Spectrum of a C*-algebra
The set of unitary equivalence classes of irreducible representations of the 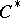 -algebra. The spectrum can be topologized if one declares that the closure of a subset is the family of all (equivalence classes of) representations whose kernels contain the intersection of the kernels of all the representations of this subset. For a commutative
-algebra. The spectrum can be topologized if one declares that the closure of a subset is the family of all (equivalence classes of) representations whose kernels contain the intersection of the kernels of all the representations of this subset. For a commutative 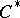 -algebra, the resulting topological space coincides with the space of characters (which is homeomorphic to the space of maximal ideals, cf. Character of a
-algebra, the resulting topological space coincides with the space of characters (which is homeomorphic to the space of maximal ideals, cf. Character of a 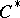 -algebra; Maximal ideal). In the general case, the spectrum of a
-algebra; Maximal ideal). In the general case, the spectrum of a 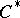 -algebra is the basis for decomposing its representations into direct integrals of irreducible representations.
-algebra is the basis for decomposing its representations into direct integrals of irreducible representations.
References
| [1] | J. Dixmier, "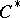 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
Comments
This topology on the spectrum of a 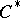 -algebra is called the hull-kernel topology, or Jacobson topology.
-algebra is called the hull-kernel topology, or Jacobson topology.
References
| [a1] | W. Arveson, "An invitation to 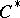 -algebras" , Springer (1976) pp. Chapts. 3–4 -algebras" , Springer (1976) pp. Chapts. 3–4 |
| [a2] | G.K. Pedersen, "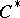 -algebras and their automorphism groups" , Acad. Press (1979) pp. §4.1 -algebras and their automorphism groups" , Acad. Press (1979) pp. §4.1 |
Spectrum of a C*-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectrum_of_a_C*-algebra&oldid=15237