Spectral theory
of linear operators
The branch of functional analysis in which one studies the structure of a linear operator on the basis of its spectral properties (such as the location of the spectrum, the behaviour of the resolvent and the asymptotics of its eigenvalues). By a description of the structure of an operator one usually means one of the following: the determination of an equivalent operator on a prescribed class of concrete (often functional) models; a specific method of reconstructing it from a class of simpler operators (for example, in the form of a direct sum or direct integral); the discovery of a basis in which the matrix of the operator has its simplest form, the proof of completeness of the system of root vectors; a complete description of the lattice of invariant subspaces; the identification of maximal chains of invariant subspaces (triangular representation); or the construction of a sufficiently wide functional calculus.
A very popular (and productive) idea in spectral theory is that of decomposing an operator into a direct sum of operators corresponding to a partition of its spectrum. The first results of this sort (for infinite-dimensional spaces) were obtained by F. Riesz (1909), who proposed the following construction. Let  be a bounded linear operator on a Banach space
be a bounded linear operator on a Banach space  with spectrum
with spectrum  and resolvent
and resolvent 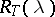 (that is,
(that is,  ,
, 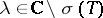 ). Then the formula
). Then the formula
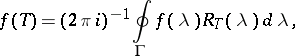 |
where 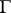 is an arbitrary contour enclosing
is an arbitrary contour enclosing 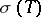 , defines a functional calculus on the algebra of germs of functions holomorphic in a neighbourhood of
, defines a functional calculus on the algebra of germs of functions holomorphic in a neighbourhood of 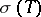 . If
. If 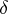 is an open-and-closed subset of
is an open-and-closed subset of  and
and 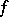 is the function equal to 1 on
is the function equal to 1 on 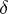 and to
and to  on
on 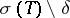 , then one obtains a projection operator
, then one obtains a projection operator 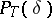 which commutes with
which commutes with 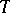 and satisfies
and satisfies 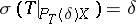 .
.
A more general spectral theory is based on the concept of a spectral subspace. The spectral manifold of 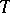 corresponding to a closed subset
corresponding to a closed subset  is defined as the set
is defined as the set 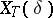 of all vectors
of all vectors 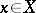 that have a local resolvent in
that have a local resolvent in 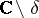 (that is, an analytic
(that is, an analytic 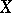 -valued function
-valued function 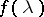 satisfying the condition
satisfying the condition 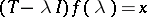 ,
, 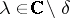 ); a spectral subspace is the closure of a spectral manifold. If any two local resolvents of the same vector coincide on the intersection of their domains of definition (this means that the local resolvent of the zero vector is equal to zero, which holds, for example, for all operators without eigenvalues), then one says that the operator has the unique extension property. In this case, for every
); a spectral subspace is the closure of a spectral manifold. If any two local resolvents of the same vector coincide on the intersection of their domains of definition (this means that the local resolvent of the zero vector is equal to zero, which holds, for example, for all operators without eigenvalues), then one says that the operator has the unique extension property. In this case, for every 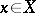 there is a local resolvent with maximal domain of definition, whose complement is called the local spectrum of
there is a local resolvent with maximal domain of definition, whose complement is called the local spectrum of 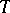 at the vector
at the vector  and is written
and is written  . Thus, for an operator
. Thus, for an operator 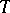 possessing the unique extension property,
possessing the unique extension property,
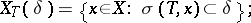 |
if 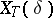 is closed, then
is closed, then 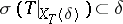 . In the general case the analogous statement about inclusion of spectral subspaces is false. Spectral subspaces satisfy the duality condition
. In the general case the analogous statement about inclusion of spectral subspaces is false. Spectral subspaces satisfy the duality condition  (where
(where 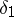 and
and 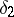 are disjoint closed sets), but the other natural condition
are disjoint closed sets), but the other natural condition 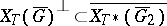 (where
(where 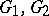 are open and
are open and 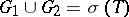 ) may be violated. This inclusion becomes valid if one replaces its right-hand side by the "weak spectral subspace"
) may be violated. This inclusion becomes valid if one replaces its right-hand side by the "weak spectral subspace" 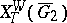 (where
(where 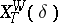 consists of the vectors
consists of the vectors 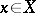 such that for every
such that for every  there is an analytic
there is an analytic 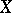 -valued function
-valued function 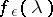 with the property that
with the property that 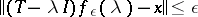 ,
, 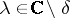 ). Sufficient conditions for stronger separability of the spectrum are known. In particular, for operators with a real spectrum the restriction
). Sufficient conditions for stronger separability of the spectrum are known. In particular, for operators with a real spectrum the restriction
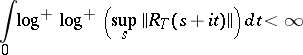 |
on the growth of the resolvent implies the existence (for any open covering of the spectrum) of a family of 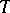 -invariant subspaces linearly generating
-invariant subspaces linearly generating 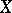 and such that the spectra of the restrictions of
and such that the spectra of the restrictions of 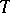 to them are inscribed in the covering. In fact, such operators belong to the class of decomposable operators, defined as operators for which the spectral manifolds are closed and which satisfy the following condition: For any open covering
to them are inscribed in the covering. In fact, such operators belong to the class of decomposable operators, defined as operators for which the spectral manifolds are closed and which satisfy the following condition: For any open covering 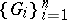 of the spectrum of
of the spectrum of 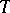 , the subspaces
, the subspaces 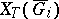 linearly generate
linearly generate 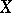 . This class of operators contains all operators with resolvents that satisfy the condition of analytic majorizability (examples are compact operators, weak perturbations of spectral operators, multipliers of Fourier series in
. This class of operators contains all operators with resolvents that satisfy the condition of analytic majorizability (examples are compact operators, weak perturbations of spectral operators, multipliers of Fourier series in 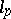 , and
, and 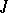 -symmetric operators), and it is stable under analytic mappings and (given certain restrictions) taking limits, and under the formation of restrictions and quotients. At the same time, an abundance of spectral subspaces (when the spectrum is sufficiently rich) guarantees the value of spectral theory. An example has been constructed of an operator which is beyond the limits of any given spectral decomposition, as the spectra of all its restrictions onto invariant subspaces coincide with the interval
-symmetric operators), and it is stable under analytic mappings and (given certain restrictions) taking limits, and under the formation of restrictions and quotients. At the same time, an abundance of spectral subspaces (when the spectrum is sufficiently rich) guarantees the value of spectral theory. An example has been constructed of an operator which is beyond the limits of any given spectral decomposition, as the spectra of all its restrictions onto invariant subspaces coincide with the interval  .
.
Even in the case of a rarefied spectrum, the restrictions of an operator onto the spectral subspaces can have a fairly complicated structure (a fine structure). Thus, every pole of the resolvent is an eigenvalue whose ascent (the maximal length of a root chain) is equal to the order of the pole; the corresponding spectral subspace is a root subspace. In the case of operators on finite-dimensional spaces this reduces to the decomposition of the operator into a direct sum of Jordan cells constructed from root chains. Analogues of the Jordan form also occupy an important place in general spectral theory; the role of Jordan cells can be played by operators with a one-point spectrum and a cyclic vector, by operators with a linearly ordered lattice of invariant subspaces (such operators are called unicellular operators; among the operators on finite-dimensional spaces this property is possessed by Jordan cells only), or by operators having simple concrete representations (models). However, the existence of such a decomposition is not universal: there are operators whose lattice of invariant subspaces and spectrum are arranged in a way too complex for one to be able to regard them as elementary "cells" , and which at the same time do not possess even one pair of disjoint invariant subspaces. For a long time it was not known whether every bounded operator (on a space of a dimension greater than 1) possesses a non-trivial invariant subspace. A positive answer to this question has been obtained for compact operators, operators that commute with compact operators, operators that are close to Hermitian or unitary operators, subnormal operators, and operators belonging to certain other special classes. In 1984 C.J. Read [8] constructed examples of operators on certain Banach spaces (including 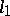 ) without invariant subspaces. For reflexive spaces the problem is still open (1990).
) without invariant subspaces. For reflexive spaces the problem is still open (1990).
Some results of finite-dimensional spectral theory have simple analogues in the spectral theory of compact operators. Thus, the spectrum of a compact operator is at most countable and its only possible accumulation point is  , the non-zero points of the spectrum are poles of the resolvent, the root subspaces are finite-dimensional, and the adjoint operator has the same structure of restrictions onto the root subspaces. However, even in the case when the point spectrum is sufficiently rich and the root vectors of
, the non-zero points of the spectrum are poles of the resolvent, the root subspaces are finite-dimensional, and the adjoint operator has the same structure of restrictions onto the root subspaces. However, even in the case when the point spectrum is sufficiently rich and the root vectors of 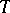 span the whole of
span the whole of 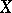 (in such cases one says that
(in such cases one says that 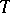 is a complete operator), the decomposition of
is a complete operator), the decomposition of 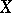 into a direct of sum of root subspaces may not be valid, due to geometric singularities of their mutual location.
into a direct of sum of root subspaces may not be valid, due to geometric singularities of their mutual location.
If 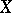 is a Hilbert space (in this case one writes
is a Hilbert space (in this case one writes 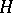 instead of
instead of  ), then every compact operator
), then every compact operator 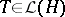 can be represented as the sum of a series
can be represented as the sum of a series
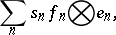 |
that is,
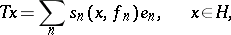 |
where 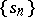 is a non-increasing sequence of positive numbers and
is a non-increasing sequence of positive numbers and 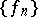 ,
, 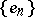 are orthonormal systems. The numbers
are orthonormal systems. The numbers  are called the singular numbers, or
are called the singular numbers, or  -numbers, of
-numbers, of  ; they coincide with the eigenvalues of the operator
; they coincide with the eigenvalues of the operator 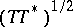 , enumerated in decreasing order, taking multiplicities into account. Moreover,
, enumerated in decreasing order, taking multiplicities into account. Moreover,  , where
, where 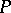 ranges over the set of projectors of co-rank
ranges over the set of projectors of co-rank  (a minimax characterization of singular numbers), and
(a minimax characterization of singular numbers), and 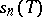 coincides with the distance from
coincides with the distance from 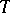 to the set of operators of rank
to the set of operators of rank  , which expresses numerically the correspondence between the rate of decrease of the singular numbers of the operator and its proximity to operators of finite rank. Based on this there are estimates for the singular numbers of sums and products, from which it follows that specific conditions on the rate of decrease of
, which expresses numerically the correspondence between the rate of decrease of the singular numbers of the operator and its proximity to operators of finite rank. Based on this there are estimates for the singular numbers of sums and products, from which it follows that specific conditions on the rate of decrease of  -numbers distinguish ideals in the algebra of operators. In particular,
-numbers distinguish ideals in the algebra of operators. In particular,
 |
is an ideal which, when 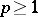 , is a Banach space with respect to the norm
, is a Banach space with respect to the norm 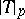 . The space
. The space  is a Hilbert space, and its elements are called Hilbert–Schmidt operators; for any
is a Hilbert space, and its elements are called Hilbert–Schmidt operators; for any 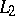 -realization of
-realization of 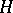 there is a representation of all Hilbert–Schmidt operators as integral operators with square-summable kernels. Operators in
there is a representation of all Hilbert–Schmidt operators as integral operators with square-summable kernels. Operators in 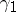 are called nuclear or trace-class operators: the trace defined on the ideal of operators of finite rank extends to a continuous functional on
are called nuclear or trace-class operators: the trace defined on the ideal of operators of finite rank extends to a continuous functional on 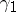 whose value on any operator coincides with the sum of (the series of) the diagonal elements of its matrix, and also with the sum of its eigenvalues. For operators of the form
whose value on any operator coincides with the sum of (the series of) the diagonal elements of its matrix, and also with the sum of its eigenvalues. For operators of the form 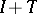 , where
, where 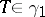 , one can define the concept of a determinant (the infinite product of the eigenvalues). The function
, one can define the concept of a determinant (the infinite product of the eigenvalues). The function 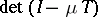 is called the characteristic determinant of
is called the characteristic determinant of 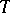 . This is a natural generalization of the characteristic polynomial of a matrix, and since there are suitable estimates, it plays a useful role in the spectral theory of nuclear operators. In particular, the resolvent of an operator
. This is a natural generalization of the characteristic polynomial of a matrix, and since there are suitable estimates, it plays a useful role in the spectral theory of nuclear operators. In particular, the resolvent of an operator 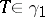 is related to the characteristic determinant by the formula (E. Fredholm, 1903)
is related to the characteristic determinant by the formula (E. Fredholm, 1903)
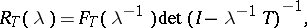 |
where 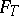 is an entire operator-function whose coefficients are expressed in terms of "partial traces" of
is an entire operator-function whose coefficients are expressed in terms of "partial traces" of 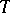 . The formulas and estimates for the resolvent obtained in this way carry over to operators in
. The formulas and estimates for the resolvent obtained in this way carry over to operators in 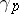 ,
, 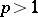 (which is important in applications), and lead to the following tests of completeness: 1) if
(which is important in applications), and lead to the following tests of completeness: 1) if 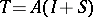 , where
, where 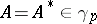 ,
, 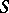 is compact and
is compact and 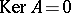 , then
, then 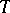 is complete (Keldysh' theorem; it has many applications in the spectral theory of differential operators); 2) if
is complete (Keldysh' theorem; it has many applications in the spectral theory of differential operators); 2) if 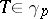 and the range of values of the quadratic form
and the range of values of the quadratic form 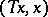 is contained in some angle of size
is contained in some angle of size 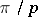 , then
, then 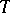 is complete.
is complete.
Compact operators whose spectra consist of the single point 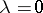 (a condition opposite to that of completeness) are called Volterra operators, in view of the fact that the Volterra integral operators
(a condition opposite to that of completeness) are called Volterra operators, in view of the fact that the Volterra integral operators
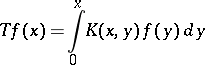 |
are their prototypes. More precisely, every Hilbert–Schmidt Volterra operator is unitarily equivalent to a Volterra integral operator on a space of vector-functions; operators not belonging to 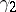 have models whose kernels are generalized functions. Such integral representations are analogues of triangular representations of matrices. Techniques for integrating operator-functions by a chain of projectors have been developed and on this basis an abstract triangular representation has been obtained for a Volterra operator:
have models whose kernels are generalized functions. Such integral representations are analogues of triangular representations of matrices. Techniques for integrating operator-functions by a chain of projectors have been developed and on this basis an abstract triangular representation has been obtained for a Volterra operator:
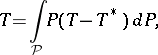 |
where  is a maximal chain of
is a maximal chain of 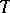 -invariant projectors. This has led to a refinement and generalization of the basic theorem in the theory of integral representations, to a proof of important relations between the distributions of the eigenvalues of the Hermitian components of Volterra operators that are close to the identity, to the construction of triangular factorizations of operators, and to the establishment of a connection between spectral theory and certain questions in the theory of boundary value problems for canonical systems of differential equations (in particular, it has enabled one to use operator methods to investigate the question of stability of such systems).
-invariant projectors. This has led to a refinement and generalization of the basic theorem in the theory of integral representations, to a proof of important relations between the distributions of the eigenvalues of the Hermitian components of Volterra operators that are close to the identity, to the construction of triangular factorizations of operators, and to the establishment of a connection between spectral theory and certain questions in the theory of boundary value problems for canonical systems of differential equations (in particular, it has enabled one to use operator methods to investigate the question of stability of such systems).
The longstanding problem of the existence of chains of rank 1 for an arbitrary compact operator, i.e. of having a cyclic vector, has been solved in the negative. The existence of invariant chains of rank 1 has been proved for dissipative operators with a nuclear imaginary component, and as a result their triangular representations have a more complete form. There is also a theory of Jordan representations for such operators, and this is consistent with the classical (finite-dimensional) case: Every operator decomposes into a quasi-direct sum of unicellular operators, where the condition of being unicellular in this class of operators is equivalent to the existence of a cyclic vector. In this theory, a central role is played by the concept of a characteristic operator-function.
In close analogy with geometric constructions in the theory of unitary dilations, the concept of the characteristic operator-function of contraction (that is, of an operator whose norm does not exceed one) lies at the heart of the spectral theory of this class of operators. This characteristic operator-function of 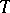 is a function
is a function 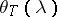 defined in the open unit disc
defined in the open unit disc 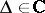 , taking values in the space of operators from
, taking values in the space of operators from 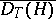 to
to 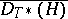 (where
(where 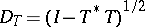 ) and satisfying the relation
) and satisfying the relation
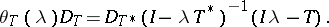 |
The characteristic operator-function is analytic in 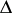 and is contractive:
and is contractive: 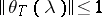 . If
. If 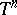 and
and 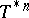 tend to zero in the strong operator topology (such operators form the class
tend to zero in the strong operator topology (such operators form the class 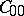 ), then
), then  is an inner function, that is, its boundary values on
is an inner function, that is, its boundary values on 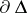 are almost-everywhere equal to 1. Conversely, for any inner operator-valued function
are almost-everywhere equal to 1. Conversely, for any inner operator-valued function 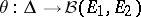 one can construct the contraction
one can construct the contraction 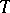 for which
for which 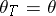 by restricting the operator of multiplication by
by restricting the operator of multiplication by 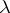 on the Hardy space
on the Hardy space 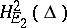 to the orthogonal complement
to the orthogonal complement 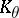 of the subspace
of the subspace 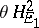 . This construction, called the functional contraction model, enables one to translate problems of spectral theory into the language of classical function theory, where they take the form of problems of interpolation, rational approximation, analytic continuation, and special factorization, among others. The functional model can be used to develop a richer functional calculus by defining for
. This construction, called the functional contraction model, enables one to translate problems of spectral theory into the language of classical function theory, where they take the form of problems of interpolation, rational approximation, analytic continuation, and special factorization, among others. The functional model can be used to develop a richer functional calculus by defining for 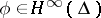 the operator
the operator 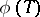 as the restriction to
as the restriction to 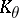 of the operator of multiplication by
of the operator of multiplication by 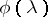 (the condition that
(the condition that 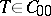 is not necessary, for
is not necessary, for 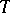 it is important to be completely non-unitary). If this calculus is not injective, that is, if
it is important to be completely non-unitary). If this calculus is not injective, that is, if 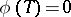 for some function
for some function 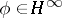 ,
, 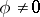 , then
, then 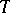 is called a contraction of class
is called a contraction of class 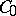 . A contraction
. A contraction 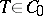 possesses a minimal inner function
possesses a minimal inner function 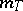 (the generator of the ideal of all functions annihilating
(the generator of the ideal of all functions annihilating  );
);  is an analogue of the minimal polynomial of a matrix: it determines many of the spectral properties of
is an analogue of the minimal polynomial of a matrix: it determines many of the spectral properties of 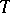 . Thus, a contraction
. Thus, a contraction 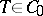 is complete if and only if
is complete if and only if  is a Blaschke product (and in this case
is a Blaschke product (and in this case 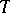 admits spectral synthesis). The point spectrum
admits spectral synthesis). The point spectrum 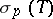 of a contraction
of a contraction 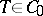 coincides with the set of zeros of
coincides with the set of zeros of 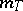 , and
, and 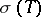 is obtained from
is obtained from 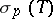 by the adjunction of those points of the boundary
by the adjunction of those points of the boundary 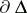 to which
to which 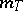 cannot be analytically continued. The fact that the contractions in
cannot be analytically continued. The fact that the contractions in 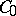 have an at most countable spectrum in
have an at most countable spectrum in 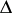 indicates the restrictions of this class. On the other hand, it contains, for example, all contractions whose deficiency operators
indicates the restrictions of this class. On the other hand, it contains, for example, all contractions whose deficiency operators 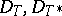 are nuclear. If
are nuclear. If 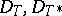 are operators of rank 1, then the functional model operates on the classical Hardy space
are operators of rank 1, then the functional model operates on the classical Hardy space 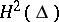 and is completely determined by the scalar inner function
and is completely determined by the scalar inner function  ; in this case one writes
; in this case one writes 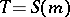 . The spectral theory of the contractions
. The spectral theory of the contractions 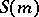 is most closely akin to that of analytic functions and has been studied the most. These contractions play the role of Jordan cells in the spectral theory of contractions in
is most closely akin to that of analytic functions and has been studied the most. These contractions play the role of Jordan cells in the spectral theory of contractions in 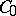 , in view of the fact that every contraction
, in view of the fact that every contraction 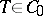 is quasi-similar to a direct sum
is quasi-similar to a direct sum 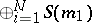 . The more usual Jordan decomposition (into unicellular operators) for a
. The more usual Jordan decomposition (into unicellular operators) for a  is not always possible.
is not always possible.
References
| [1a] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral operators" , 3 , Interscience (1971) MR0412888 |
| [1b] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , 2 , Interscience (1963) MR0188745 |
| [2] | H. Radjavi, P. Rosenthal, "Invariant subspaces" , Springer (1973) MR0367682 Zbl 0269.47003 |
| [3] | I. Colojoară, C. Foiaş, "Theory of generalized spectral operators" , Gordon & Breach (1968) MR0394282 Zbl 0189.44201 |
| [4] | I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Introduction to the theory of linear nonselfadjoint operators" , Transl. Math. Monogr. , 18 , Amer. Math. Soc. (1969) (Translated from Russian) MR0246142 Zbl 0181.13504 |
| [5] | I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Theory and applications of Volterra operators in Hilbert space" , Amer. Math. Soc. (1970) (Translated from Russian) MR0264447 Zbl 0194.43804 |
| [6] | B. Szökefalvi-Nagy, Ch. Foiaş, "Harmonic analysis of operators on Hilbert space" , North-Holland (1970) (Translated from French) MR275190 |
| [7] | N.K. Nikol'skii, "Treatise on the shift operator: spectral function theory" , Springer (1986) (Translated from Russian) Zbl 0587.47036 |
| [8] | C.J. Read, "A solution to the invariant subspace problem" Bull. London Math. Soc. , 16 : 4 (1984) pp. 337–401 MR0749447 Zbl 0566.47003 |
Comments
For the notions of a root vector and root subspace of a linear operator cf. Root vector.
A root chain (corresponding to the root 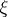 ) of a linear operator
) of a linear operator 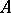 is a sequence of non-zero vectors
is a sequence of non-zero vectors  such that
such that 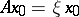 ,
, 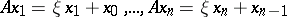 . It is also called a Jordan chain, [a1].
. It is also called a Jordan chain, [a1].
Quite generally, the ascent of a linear operator 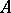 on a Banach space is defined as the smallest integer
on a Banach space is defined as the smallest integer  such that
such that 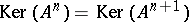 , and then
, and then 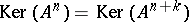 for all
for all 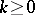 . If no such integer
. If no such integer  exists, the ascent
exists, the ascent 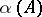 of
of 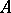 is set equal to
is set equal to 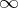 .
.
Let 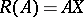 denote the range of an operator
denote the range of an operator 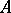 on a Banach space
on a Banach space 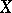 . The descent of a linear operator
. The descent of a linear operator  is defined as the smallest integer such that
is defined as the smallest integer such that 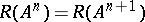 , and then
, and then 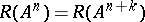 for all
for all 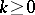 . If no such
. If no such  exists, the descent
exists, the descent 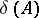 of
of 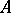 is set equal to
is set equal to 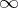 .
.
If 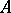 is a bounded linear operator and
is a bounded linear operator and 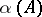 and
and 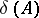 are both finite, then
are both finite, then 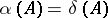 (
(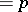 ) and
) and 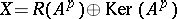 . Especially for finite-dimensional Banach spaces this is known as the Fitting decomposition of
. Especially for finite-dimensional Banach spaces this is known as the Fitting decomposition of  corresponding to
corresponding to  . The operator
. The operator  correspondingly becomes a direct sum of a bijective operator
correspondingly becomes a direct sum of a bijective operator 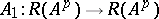 and a nilpotent operator
and a nilpotent operator 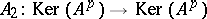 ; this is called the Fitting decomposition of the operator
; this is called the Fitting decomposition of the operator 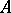 . Fitting's lemma applies also in other contexts. For instance, for a module endomorphism
. Fitting's lemma applies also in other contexts. For instance, for a module endomorphism 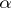 of a module
of a module  of finite length there is an
of finite length there is an  such that
such that 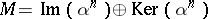 .
.
References
| [a1] | M.S. Birman, M.Z. Solomyak, "Spectral theory of selfadjoint operators in Hilbert space" , Reidel (1987) pp. Chapt. 3, §5 (Translated from Russian) MR1192782 |
| [a2] | H.R. Dowson, "Spectral theory of linear operators" , Acad. Press (1978) MR0511427 Zbl 0384.47001 |
Spectral theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_theory&oldid=24566