Spectral resolution
spectral function, resolution of the identity
A monotone mapping 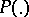 which is left-continuous in the strong operator topology, from the real line into the set of orthogonal projectors on a Hilbert space, and satisfying the conditions
which is left-continuous in the strong operator topology, from the real line into the set of orthogonal projectors on a Hilbert space, and satisfying the conditions
 |
Every self-adjoint (i.e. taking self-adjoint values) strongly countably-additive Borel spectral measure  on the line defines a spectral resolution by the formula
on the line defines a spectral resolution by the formula  , and for every spectral resolution there is a unique spectral measure defining it.
, and for every spectral resolution there is a unique spectral measure defining it.
The concept of a spectral resolution is fundamental in the spectral theory of self-adjoint operators: By the spectral decomposition theorem (cf. Spectral decomposition of a linear operator), every such operator has an integral representation  , where
, where  is some spectral resolution. An analogous role in the theory of symmetric operators is played by the concept of a generalized spectral resolution, which is a mapping from the real line into the set of non-negative operators that satisfies all the conditions imposed on spectral resolutions, except that the values need not be projectors. Every generalized spectral resolution can be extended to a spectral resolution on a larger space (Naimark's theorem).
is some spectral resolution. An analogous role in the theory of symmetric operators is played by the concept of a generalized spectral resolution, which is a mapping from the real line into the set of non-negative operators that satisfies all the conditions imposed on spectral resolutions, except that the values need not be projectors. Every generalized spectral resolution can be extended to a spectral resolution on a larger space (Naimark's theorem).
References
| [1] | N.I. Akhiezer, I.M. Glazman, "Theory of linear operators in Hilbert space" , 1–2 , Pitman (1981) (Translated from Russian) |
| [2] | M.A. Naimark, "Self-adjoint extensions of the second kind of a symmetric operator" Izv. Akad. Nauk SSSR Ser. Mat. , 4 : 1 (1940) pp. 53–104 (In Russian) (English abstract) |
Spectral resolution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_resolution&oldid=16434