Spectral radius
of an element of a Banach algebra
The radius 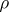 of the smallest closed disc in the plane that contains the spectrum of this element (cf. Spectrum of an element). The spectral radius of an element
of the smallest closed disc in the plane that contains the spectrum of this element (cf. Spectrum of an element). The spectral radius of an element  is connected with the norms of its powers by the formula
is connected with the norms of its powers by the formula
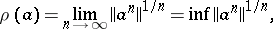 |
which, in particular, implies that 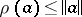 . The spectral radius of a bounded linear operator on a Banach space is the spectral radius of it regarded as an element of the Banach algebra of all operators. In a Hilbert space, the spectral radius of an operator is equal to the greatest lower bound of the norms of the operators similar to it (see [2]):
. The spectral radius of a bounded linear operator on a Banach space is the spectral radius of it regarded as an element of the Banach algebra of all operators. In a Hilbert space, the spectral radius of an operator is equal to the greatest lower bound of the norms of the operators similar to it (see [2]):
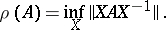 |
If the operator is normal, then  (cf. Normal operator).
(cf. Normal operator).
As a function of the elements of a Banach algebra, the spectral radius is upper semi-continuous (but not, in general, continuous). The subharmonicity of the spectral radius has been proved [3]. (This means that if 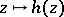 is a holomorphic mapping of some domain
is a holomorphic mapping of some domain 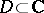 into a Banach algebra
into a Banach algebra 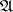 , then
, then 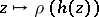 is a subharmonic function.)
is a subharmonic function.)
References
| [1] | M.A. Naimark, "Normed rings" , Reidel (1959) (Translated from Russian) |
| [2] | P.R. Halmos, "A Hilbert space problem book" , Springer (1980) |
| [3] | E. Vesentini, "On the subharmonicity of the spectral radius" Boll. Union. Mat. Ital. , 1 (1968) pp. 427–429 |
| [4] | V. Ptak, "On the spectral radius in Banach algebras with involution" Bull. London Math. Soc. , 2 (1970) pp. 327–334 |
Comments
References
| [a1] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
Spectral radius. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_radius&oldid=15490