Spectral function of a stationary stochastic process
spectral function of a homogeneous random field in an  -dimensional space, spectral distribution function
-dimensional space, spectral distribution function
A function of the frequency 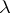 , or of a wave vector
, or of a wave vector 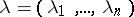 , respectively, occurring in the spectral decomposition of the covariance function of a stochastic process which is stationary in the wide sense, or of a random field in an
, respectively, occurring in the spectral decomposition of the covariance function of a stochastic process which is stationary in the wide sense, or of a random field in an  -dimensional space which is homogeneous in the wide sense, respectively (cf. Spectral decomposition of a random function). The class of spectral functions of stationary stochastic processes coincides with that of all bounded monotonically non-decreasing functions
-dimensional space which is homogeneous in the wide sense, respectively (cf. Spectral decomposition of a random function). The class of spectral functions of stationary stochastic processes coincides with that of all bounded monotonically non-decreasing functions 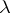 , and the class of spectral functions of homogeneous random fields coincides with the class of functions in
, and the class of spectral functions of homogeneous random fields coincides with the class of functions in  variables
variables 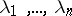 differing only by a non-negative constant multiplier from
differing only by a non-negative constant multiplier from  -dimensional probability distribution functions.
-dimensional probability distribution functions.
Spectral function of a stationary stochastic process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_function_of_a_stationary_stochastic_process&oldid=13090