Spectral density
of a stationary stochastic process or of a homogeneous random field in  -dimensional space
-dimensional space
The Fourier transform of the covariance function of a stochastic process which is stationary in the wide sense (cf. Stationary stochastic process; Random field, homogeneous). Stationary stochastic processes and homogeneous random fields for which the Fourier transform of the covariance function exists are called processes with a spectral density.
Let
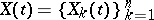 |
be an  -dimensional stationary stochastic process, and let
-dimensional stationary stochastic process, and let
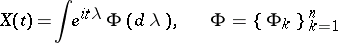 |
be its spectral representation (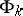 is the spectral measure corresponding to the
is the spectral measure corresponding to the 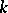 -th component
-th component 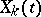 of the multi-dimensional stochastic process
of the multi-dimensional stochastic process 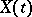 ). The range of integration is
). The range of integration is  in the case of discrete time
in the case of discrete time 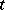 , and
, and 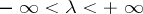 in the case of continuous time
in the case of continuous time 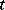 . The process
. The process 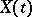 has a spectral density
has a spectral density
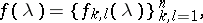 |
if all the elements
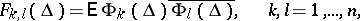 |
of the spectral measure 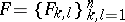 are absolutely continuous and if
are absolutely continuous and if
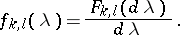 |
In particular, if the relation
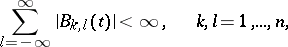 |
holds for 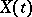 ,
, 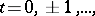 where
where
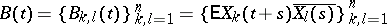 |
is the covariance function of  , then
, then 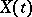 has a spectral density and
has a spectral density and
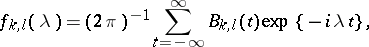 |
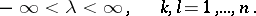 |
The situation is similar in the case of processes 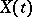 in continuous time
in continuous time 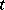 . The spectral density
. The spectral density 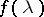 is sometimes called the second-order spectral density, in contrast to higher spectral densities (see Spectral semi-invariant).
is sometimes called the second-order spectral density, in contrast to higher spectral densities (see Spectral semi-invariant).
A homogeneous  -dimensional random field
-dimensional random field 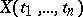 has a spectral density
has a spectral density 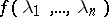 if its spectral resolution
if its spectral resolution 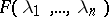 possesses the property that its mixed derivative
possesses the property that its mixed derivative 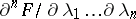 exists almost-everywhere, and then
exists almost-everywhere, and then
 |
and
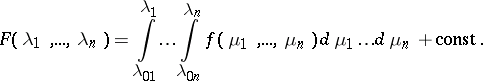 |
References
| [1] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) |
| [2] | Yu.A. Rozanov, "Stationary random processes" , Holden-Day (1967) (Translated from Russian) |
Spectral density. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_density&oldid=13166