Spanier-Whitehead duality(2)
Whitehead–Spanier duality
Let  be a CW-spectrum (see Spectrum of spaces) and consider
be a CW-spectrum (see Spectrum of spaces) and consider
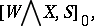 |
where  is another CW-spectrum,
is another CW-spectrum,  is the smash product of
is the smash product of  and
and  (see [a2], Sect. III.4),
(see [a2], Sect. III.4),  is the sphere spectrum, and
is the sphere spectrum, and  denotes stable homotopy classes of mappings of spectra. With
denotes stable homotopy classes of mappings of spectra. With  fixed, this is a contravariant functor of
fixed, this is a contravariant functor of 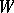 which satisfies the axioms of E.H. Brown (see [a1]) and which is hence representable by a spectrum
which satisfies the axioms of E.H. Brown (see [a1]) and which is hence representable by a spectrum 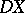 , the Spanier–Whitehead dual of
, the Spanier–Whitehead dual of 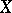 .
.
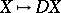 is a contravariant functor with many duality properties. E.g.,
is a contravariant functor with many duality properties. E.g.,
i) 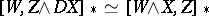 ;
;
ii) 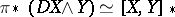 ;
;
iii) 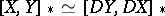 ;
;
iv)  ;
;
v) for a (generalized) homology theory  there is a natural isomorphism between
there is a natural isomorphism between 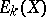 and
and 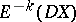 .
.
In many ways 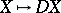 is similar to the linear duality functor
is similar to the linear duality functor 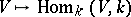 for finite-dimensional vector spaces over a field
for finite-dimensional vector spaces over a field 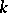 .
.
For 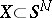 , the
, the 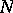 -dimensional sphere, the classical Alexander duality theorem says that
-dimensional sphere, the classical Alexander duality theorem says that 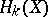 is isomorphic to
is isomorphic to 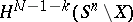 , and this forms the basic intuitive geometric idea behind Spanier–Whitehead duality.
, and this forms the basic intuitive geometric idea behind Spanier–Whitehead duality.
For more details, see [a2], Sect. II.5, and [a3], Sect. 5.2. For an equivariant version, see [a4], p. 300ff.
References
| [a1] | E.H. Brown, "Cohomology theories" Ann. of Math. , 75 (1962) pp. 467–484 |
| [a2] | J.F. Adams, "Stable homotopy and generalised homology" , Chicago Univ. Press (1974) |
| [a3] | D.C. Ravenel, "The stable homotopy theory of finite complexes" I.M. James (ed.) , Handbook of Algebraic Topology , Elsevier (1995) pp. 325–396 |
| [a4] | J.P.C. Greenlees, J.P. May, "Equivariant stable homotopy theory" I.M. James (ed.) , Handbook of Algebraic Topology , Elsevier (1995) pp. 227–324 |
Spanier-Whitehead duality(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spanier-Whitehead_duality(2)&oldid=18478