Space-time
A term denoting a geometric structure that describes the spatial and temporal relations in those physical theories in which these relations are considered as interdependent (these theories are usually called relativistic). The first concept of space-time arose in the formulation and systematization of basic assumptions of relativity theory. The space-time of this theory is the four-dimensional pseudo-Euclidean space 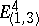 with line element
with line element
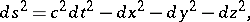 |
where 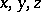 are the space coordinates,
are the space coordinates, 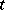 is the time coordinate and
is the time coordinate and  is the velocity of light. This coordinate system is called in physics the Lorentz coordinate system (cf. Galilean coordinate system) and corresponds to an inertial system. The transition between two different Lorentz coordinate systems, corresponding to observations in inertial systems moving with respect to another, is effected by means of a Lorentz transformation. The fact that the time coordinate in the new coordinate system turns out to be expressed both in terms of the time as well as in terms of the space coordinates of the old system, reflects the interdependence of spatial and temporal relations in special relativity theory. The space-time of special relativity theory is also called Minkowski space-time, or Lorentz space-time.
is the velocity of light. This coordinate system is called in physics the Lorentz coordinate system (cf. Galilean coordinate system) and corresponds to an inertial system. The transition between two different Lorentz coordinate systems, corresponding to observations in inertial systems moving with respect to another, is effected by means of a Lorentz transformation. The fact that the time coordinate in the new coordinate system turns out to be expressed both in terms of the time as well as in terms of the space coordinates of the old system, reflects the interdependence of spatial and temporal relations in special relativity theory. The space-time of special relativity theory is also called Minkowski space-time, or Lorentz space-time.
In general relativity theory various four-dimensional pseudo-Riemannian spaces with signature 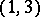 are used as space-time. The difference between the metric of such a space-time and the flat metric of the space-time of special relativity theory describes a gravitational field (cf. Gravitation). In turn, the metric of space-time is connected with the distribution and properties of gravitating bodies and fields by means of the Einstein equations.
are used as space-time. The difference between the metric of such a space-time and the flat metric of the space-time of special relativity theory describes a gravitational field (cf. Gravitation). In turn, the metric of space-time is connected with the distribution and properties of gravitating bodies and fields by means of the Einstein equations.
The emergence of the concept of space-time played an important part in overcoming the approach to space as the absolute location of bodies and to time as absolute duration, unrelated to real physical processes.
Nowadays the concept of space-time in some form or other enters the structure of the physical theories in which relativistic effects are studied (relativistic quantum mechanics, quantum field theory, etc.). In general relativity theory many types of space-time have been studied, as solutions to the Einstein equations.
The essential difference between spatial and temporal relations, from the point of view of relativistic physics, finds its expression in the presence of vectors of various natures in space-time: space-like, time-like and light-like vectors, forming cones in the tangent spaces. Correspondingly, the metric of space-time is indefinite, and space-like, time-like and light-like vectors give different signs of the scalar square. The boundary between the space-like and the time-like vectors forms an isotropic cone, whose vectors (cf. Isotropic vector) have scalar square zero and correspond to the motion of light and other particles of zero rest mass.
Many specific effects in relativity theory are related to the indefiniteness of the metric of space-time and to the presence of structures on the isotropic cones in space-time. E.g., Lorentz contraction of time is a consequence of the converse triangle inequality in a space with an indefinite metric, according to which in a two-dimensional pseudo-Euclidean space a time-like curve is always shorter than its projection on a (non-parallel) time axis.
In a lot of situations it turns out to be useful to abstract to a certain extent from the concrete structure of the metric of space-time and to consider only properties of the structures of the isotropic cones in space-time, i.e. to consider various so-called general spaces of kinematic type, or time-like spaces.
In a retrospective analysis of previous physical theories from the point of view of relativity theory, various kinds of space-time were constructed that can be conditionally put in correspondence with Newtonian mechanics (a Galilean space) and even with the physical conceptions of Aristotle (cf. [5]). These space-times are different spaces with a degenerate isotropic (light) cone (e.g. semi-Riemannian spaces). It is precisely the degeneration of the isotropic cone that allows one to regard these spaces as limit cases of the space-time of relativity theory.
References
| [1] | A. Einstein, "Die Relativitätstheorie" E. Lechner (ed.) , Die Physik , 3.3.1 , Teubner (1915) pp. 703–713 |
| [2] | H. Minkowski, "Raum und Zeit" Phys. Z. , 104 (1909) |
| [3] | E.M. Lifshits, "The classical theory of fields" , Pergamon (1975) (Translated from Russian) |
| [4] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [5] | R. Penrose, "Structure of space-time" C.M. DeWitt (ed.) J.A. Wheeler (ed.) , Batelle Rencontres 1967 Lectures in Math. Physics , Benjamin (1968) pp. 121–235 (Chapt. VII) |
Comments
References
| [a1] | A. Einstein, "The meaning of relativity" , Princeton Univ. Press (1974) |
| [a2] | J.L. Anderson, "Principles of relativity physics" , Acad. Press (1967) |
Space-time. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Space-time&oldid=32957