Space
A logical conceptual form (or structure) serving as a medium in which other forms and some structures are realized. E.g., in elementary geometry the plane or space serves as the medium in which one constructs various figures. In the majority of cases one fixes relations in space that are compatible in formal properties with the usual spatial relationships (distances between points, equality of figures, etc.), so that for such spaces one can say that they represent logical conceptual space-like forms. The first, and most important, mathematical space is the three-dimensional Euclidean space, representing an approximate abstraction of the form of real space. The general concept of "space" in mathematics is complex, owing to the result of generalization and changes in the concept of the geometry of Euclidean space. The first spaces differing from three-dimensional Euclidean space were introduced in the first half of the 19th century. These were the Lobachevskii space and the Euclidean space of arbitrary dimension (cf. Non-Euclidean geometries; Higher-dimensional geometry). The general concept of a mathematical space as a "multiple extension" , or "manifold" , was introduced in 1854 by B. Riemann. It was generalized, axiomatized and made concrete in various directions: such as, e.g., Riemannian space; Finsler space; vector space; Hilbert space; metric space, and topological space. In contemporary mathematics space is defined as a certain set of objects, which are called its points; they can be geometric objects, functions, states of a physical system, etc. By considering such a set as a space one abstracts any property of its elements and considers only those properties of their totality that can be defined by relations that are taken into account or that are introduced by definition. These relations between points and some figures, i.e. sets of points, determine the "geometry" of the space. In an axiomatic construction, the basic properties of these relations are expressed in corresponding axioms.
As examples of spaces one can mention:
1) metric spaces, in which the distance between points is defined; e.g. the space of continuous functions on the segment  , where functions
, where functions  , continuous on
, continuous on  , are taken as points, while the distance between two functions
, are taken as points, while the distance between two functions  and
and  is defined as the maximum of the moduli of their differences:
is defined as the maximum of the moduli of their differences:
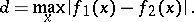 |
2) The "space of events" , playing an important part in the geometric interpretation of relativity theory. Every event is characterized by its position, coordinates  , and time
, and time  , therefore the set of all possible events is a four-dimensional space, with as "points" the events with four coordinates
, therefore the set of all possible events is a four-dimensional space, with as "points" the events with four coordinates  .
.
3) The phase spaces, considered in theoretical physics and mechanics. The phase space of a physical system is the set of all possible states of the system, which are to be regarded as the points of this space.
Comments
See also Banach space; Minkowski space; Continuous functions, space of; Space of mappings, topological.
References
| [a1] | H. Senechal (ed.) G. Fleck (ed.) , Shaping space , Birkhäuser (1988) |
| [a2] | H. Weyl, "Space-time-matter" , Dover, reprint (1950) (Translated from German) |
| [a3] | H. Weyl, "Philosophy of mathematics and natural science" , Princeton Univ. Press (1949) |
Space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Space&oldid=15588