Soliton
A solution of a non-linear evolution equation which at every moment of time is localized in a bounded domain of space, such that the size of the domain remains bounded in time while the movement of the centre of the domain can be interpreted as the movement of a particle. The soliton solution of the Korteweg–de Vries equation
 |
given by
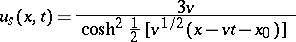 |
describes such a solitary wave, and is uniquely determined by two parameters: the velocity  and the position of the maximum at a fixed moment in time
and the position of the maximum at a fixed moment in time 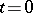 ,
,  . This equation also has
. This equation also has  -soliton solutions, which for large
-soliton solutions, which for large  (
( ) can be written approximately as the sum of
) can be written approximately as the sum of  terms
terms 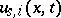 , each of which is characterized by its velocity
, each of which is characterized by its velocity 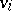 and the position of its centre
and the position of its centre 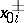 . For an
. For an  -soliton solution, the set of velocities before collision
-soliton solution, the set of velocities before collision  and after collision
and after collision 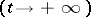 remains the same; there arise only shifts of the centres of soliton solutions
remains the same; there arise only shifts of the centres of soliton solutions  . Many non-linear evolution equations in two independent variables have been found which possess solutions with the above properties. Thus, the soliton solution of the non-linear Schrödinger equation
. Many non-linear evolution equations in two independent variables have been found which possess solutions with the above properties. Thus, the soliton solution of the non-linear Schrödinger equation
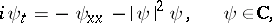 |
is uniquely determined by four parameters, and that of the sine-Gordon equation
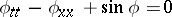 |
by two parameters  ,
,  :
:
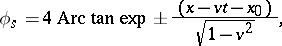 |
and there is a double soliton (breather) which is defined by four parameters.
There is an analogous situation for the Boussinesq equation
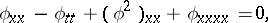 |
the Hirota equation
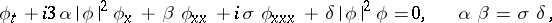 |
and others. There are also physically interesting equations with a larger number of independent variables that have soliton solutions with the above properties. For example, a soliton of the Kadomtsev–Petviashvili equation (two space variables)
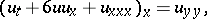 |
localized in  and
and 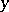 , is equal to
, is equal to
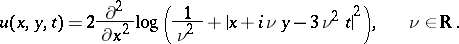 |
In physics literature, the term "soliton" means a particle-like solution of a non-linear equation of classical field theory for which energy and momentum densities remain localized in a neighbourhood of some point of space at any moment in time. Sometimes, localization can occur near lines and surfaces. These localized solutions are also called kinks or monopoles. The search for solutions of this type involves topological considerations. In particular, for several models one can successfully construct a current 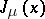 whose divergence is equal to zero independently of the equations of motion, and the corresponding integral of motion (the topological charge)
whose divergence is equal to zero independently of the equations of motion, and the corresponding integral of motion (the topological charge) 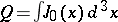 gives a lower bound for the energy functional.
gives a lower bound for the energy functional.
References
| [1] | A.C. Scott, F.Y.F. Chu, D.W. Mclaughlin, "The soliton: a new concept in applied science" Proc. IEEE , 61 (1973) pp. 1443–1483 |
| [2] | V.I. Karpman, "Non-linear waves in dispersing media" , Moscow (1973) (In Russian) |
| [3] | B.A. Dubrovin, V.B. Matveev, S.P. Novikov, "Non-linear equations of Korteweg–de Vries type, finite-zone linear operators, and abelian varieties" Russian Math. Surveys , 31 : 1 (1976) pp. 59–146 Uspekhi Mat. Nauk , 31 (1976) pp. 55–136 |
| [4] | M.J. Ablowitz, H. Segur, "Solitons and inverse scattering transform" , SIAM (1981) |
| [5] | F. Calogero, "Spectral transform and solitons" , 1 , North-Holland (1982) |
| [6] | L.D. Faddeev, L.A. Takhtadzhyan, "Hamiltonian methods in the theory of solitons" , Springer (1987) (Translated from Russian) |
Comments
The term "soliton" was coined by C.S. Gardner, J.M. Greene, M.D. Kruskal, and R.M. Miura [a3], the originators of the inverse scattering method, to describe solitary wave solutions of the KdV equation (Korteweg–de Vries equation) with particle-like behaviour in the sense that when two of these meet, travelling at different velocities, then, after some confused interaction pattern, both, after having passed through each other, emerge unchanged in form and velocity (but there is a phase shift).
There are fundamental connections between the boundary value problems of analytic function theory and soliton equations. One such connection is provided by the so-called Zakharov–Shabat dressing method [a5], cf. also [a4], [a6], which associates a new solution (a "dressed-up" solution) to a solution of a family of Riemann–Hilbert boundary value problems defined by an old solution (which can be trivial).
References
| [a1] | A.C. Newell, "Solitons in mathematics and physics" , SIAM (1985) |
| [a2] | M. Toda, "Nonlinear waves and solitons" , Kluwer (1989) |
| [a3] | C.S. Gardner, J.M. Greene, M.D. Kruskal, R.M. Miura, "Method for solving the Korteweg–de Vries equation" Phys. Rev. Lett. , 19 (1967) pp. 1095–1097 |
| [a4] | V.E. Zakharov, S.V. Manakov, "Soliton theory" Soviet Sci. Rev. Sect. A: Phys. Rev. , 1 (1979) pp. 133–190 |
| [a5] | V.E. Zakharov, A.B. Shabat, "Integration of the nonlinear equations of mathematical physics by the method of the inverse scattering problem II" Funct. Anal. Appl. , 13 : 3 (1979) pp. 166–174 Funkts. Anal. i Prilozh. , 13 : 3 (1979) pp. 13–22 |
| [a6] | C. Rebbi (ed.) G. Soliani (ed.) , Solitons and particles , World Sci. (1984) |
| [a7] | S. Novikov, S.V. Manakov, L.P. Pitaevskii, V.E. Zakharov, "Theory of solitons" , Plenum (1984) (Translated from Russian) |
| [a8] | D.V. Chudnovsky (ed.) G. Chudnovsky (ed.) , The Riemann problem, complete integrability and arithmetic applications , Lect. notes in math. , 925 , Springer (1982) |
| [a9] | R.K. Dodd, J.C. Eilbeck, J.D. Gibbon, H.C. Morris, "Solitons and nonlinear wave equations" , Acad. Press (1982) |
| [a10] | A.S. Davydov, "Solitons in molecular systems" , Kluwer (1991) (Translated from Russian) |
| [a11] | V.G. Makhankov, "Soliton phenomenology" , Kluwer (1991) (Translated from Russian) |
Soliton. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Soliton&oldid=48747