Socle
of a module
The sum of all its simple submodules. When there are none, the socle is taken to be 0. In accordance with this definition one can consider in a ring its left and right socle. Each of them turns out to be a two-sided ideal that is invariant under all endomorphisms of the ring. The socle can be represented as a direct sum of simple modules. Completely-reducible modules (semi-simple modules) can be characterized as modules that coincide with their socle.
Comments
A submodule 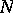 of a module
of a module  is large, or essential, if
is large, or essential, if 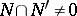 for every non-zero submodule
for every non-zero submodule 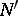 of
of 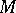 . A complement (respectively, essential complement) of
. A complement (respectively, essential complement) of 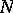 in
in  is a submodule
is a submodule  such that
such that 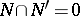 and
and  (respectively,
(respectively, 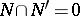 and
and 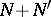 is large). A module is complemented if each submodule has a complement. Each submodule always has a (not necessarily unique) essential complement. A module is complemented if and only if it is completely reducible and hence if and only if it coincides with its socle. The socle of
is large). A module is complemented if each submodule has a complement. Each submodule always has a (not necessarily unique) essential complement. A module is complemented if and only if it is completely reducible and hence if and only if it coincides with its socle. The socle of 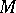 can also be defined as the intersection of all the essential submodules of
can also be defined as the intersection of all the essential submodules of 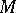 . The socle is the largest semi-simple submodule.
. The socle is the largest semi-simple submodule.
More generally, for a modular lattice 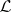 an element
an element 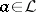 is large or essential if
is large or essential if 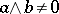 for all
for all  . The socle of a modular lattice is defined as
. The socle of a modular lattice is defined as 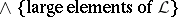 . The interval
. The interval  is a complemented lattice.
is a complemented lattice.
References
| [a1] | L.H. Rowen, "Ring theory" , 1 , Acad. Press (1988) pp. §2.4 |
| [a2] | C. Faith, "Algebra: rings, modules, and categories" , 1 , Springer (1973) pp. 367 |
Socle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Socle&oldid=18319