Smoothness, modulus of
The modulus of continuity of the derivative of order $ m \geq 1 $
of a function $ f $
defined on a Banach space $ X $,
i.e. the expression
$$ \omega _ {m} ( f, \delta , X) = $$
$$ = \ \sup _ {\begin{array}{c} h,x \in X \\ \| h \| _ {X} \leq \delta \end{array} } \left \| \sum _ {i = 0 } ^ { m } (- 1) ^ {m - i } \left ( \begin{array}{c} m \\ i \end{array} \right ) f \left ( x + ( m - 2i) { \frac{h}{2} } \right ) \right \| _ {X} , $$
where $ ( x \pm mh/2) \in X $. If $ m = 1 $, the modulus of smoothness is the ordinary modulus of continuity (cf. Continuity, modulus of) of $ f $. Basic properties of the modulus of smoothness (in the case $ X = \mathbf C $ and the space of continuous functions) are:
$$ \omega _ {m} ( f, 0, \mathbf C ) = 0; $$
$ \omega _ {m} ( f, \delta , \mathbf C ) $ does not decrease together with $ \delta $;
if $ k $ $ \geq 1 $ is an integer, then
$$ \omega _ {m} ( f, k \delta , \mathbf C ) \leq \ k ^ {m} \omega _ {m} ( f, \delta , \mathbf C ); $$
for any $ \lambda > 0 $,
$$ \omega _ {m} ( f, \lambda \delta , \mathbf C ) \leq \ ( \lambda + 1) ^ {m} \omega _ {m} ( f, \delta , \mathbf C ); $$
if $ \nu > m $, then
$$ \omega _ \nu ( f, \delta , \mathbf C ) \leq \ 2 ^ {\nu - m } \omega _ {m} ( f, \delta , \mathbf C ); $$
if $ \nu > m $, then
$$ \omega _ {m} ( f, \delta , \mathbf C ) \leq A _ {\nu , m } \delta ^ \nu \int\limits _ \delta ^ { a } \frac{\omega _ {m} ( f, u , \mathbf C ) }{u ^ {\nu + 1 } } \ du + O ( \delta ^ \nu ), $$
where $ A _ {\nu , m } $ and $ a $ are constants independent of $ f $.
Certain problems in the theory of approximation of functions can ultimately be solved only in terms of a modulus of smoothness of order $ m \geq 2 $. In the theory of approximations of functions an important class is the class of periodic continuous functions with period $ 2 \pi $ and with second-order modulus of smoothness satisfying the condition
$$ \omega _ {2} ( f, \delta , C _ {2 \pi } ) \leq \delta . $$
The modulus of continuity of such functions satisfies the condition
$$ \omega _ {1} ( f, \delta , C _ {2 \pi } ) \leq \ \left [ \frac{1}{ \mathop{\rm ln} ( \sqrt {2 } + 1) } \right ] \delta \mathop{\rm ln} { \frac \pi \delta } + O ( \delta ), $$
$ 0 < \delta \leq \pi $, and the constant $ 1/ \mathop{\rm ln} ( \sqrt {2 } + 1) $ cannot be improved [4].
References
| [1] | S.N. Bernshtein, "Sur l'ordre de la meilleure approximation des fonctions continués par de polynomes de degré donné" Mem. Publ. Classe Sci. Acad. Belgique (2) , 4 (1912) pp. 1–103 |
| [2] | A. Marchaud, "Sur les dérivées et sur les différences des fonctions de variables réelles" J. Math. Pures Appl. , 6 (1927) pp. 337–425 |
| [3] | A. Zygmund, "Smooth functions" Duke Math. J. , 12 (1945) pp. 47–76 |
| [4] | A.V. Efimov, "Estimate of the modules of continuity of a function in the class 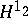 " Izv. Akad. Nauk SSSR Ser Mat. , 21 (1957) pp. 283–288 (In Russian) " Izv. Akad. Nauk SSSR Ser Mat. , 21 (1957) pp. 283–288 (In Russian) |
Comments
The modulus of smoothness $ \omega _ {m} ( f, \delta ) $ is also written in terms of symmetric differences, as $ \omega _ {m} ( f , \delta ) = \sup _ {0 < h \leq \delta } \| \Delta _ {h} ^ {m} f \| $, where
$$ \Delta _ {h} ^ {1} f ( x) = \ f \left ( x + \frac{h}{2} \right ) - f \left ( x - \frac{h}{2} \right ) $$
and
$$ \Delta _ {h} ^ {m} f ( x) = \ \Delta _ {n} ( \Delta _ {n} ^ {m-} 1 f( x)) = \ \sum _ { i= } 0 ^ { m } (- 1) ^ {m-} i \left ( \begin{array}{c} m \\ i \end{array} \right ) f \left ( x + ( m- 2i) \frac{h}{2} \right ) . $$
This gives a recurrent procedure for computing (approximations of) it.
To overcome certain shortcomings of this (classical) modulus of smoothness (especially its ability to characterize the order of the best polynomial approximation $ E _ {n} ( f ) $ to a function $ f \in L _ {p} [- 1 , 1] $), new moduli of smoothness have been introduced. They use so-called step-weight functions $ \varphi ( x) $, and are defined by
$$ \omega _ \varphi ^ {n} ( f , \delta ) _ {p} = \ \sup _ {0 < h \leq \delta } \ \| \Delta _ {h\varphi } ^ {m} f \| _ {L _ {p} } . $$
The function $ \varphi ( x) $ is chosen for the problem at hand. Note that here the increment $ h \varphi ( x) $ varies with $ x $. A basic result is that $ E _ {n} ( f ) _ {p} = O( n ^ {- \alpha } ) $ if and only if $ \omega _ \varphi ^ {m} ( f , \delta ) _ {p} = O( t ^ \alpha ) $. (Here $ 0< \alpha < m $, $ 1 \leq p \leq \infty $, $ \varphi ( x) = ( 1- x ^ {2} ) ^ {1/2} $, $ f \in L _ {p} [- 1, 1] $, and approximation is in $ L _ {p} [- 1, 1] $.) For more on such moduli, their use in $ L _ {p} $ approximation problems and in the interpolation of spaces, see [a1].
References
| [a1] | Z. Ditzian, V. Totik, "Moduli of smoothness" , Springer (1987) |
| [a2] | G.G. Lorentz, "Approximation of functions" , Holt, Rinehart & Winston (1966) |
Smoothness, modulus of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Smoothness,_modulus_of&oldid=48741