Smooth space

A normed space 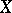in which for any point with there exists a unique functional 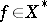such that 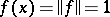. A space 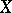is smooth if and only if its norm has a Gâteaux differential at all points with .

Comments

Let 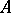be a solid (i.e. 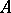has a non-empty interior) convex set in a real linear topological space. A point 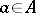is a support point if there is a hyperplane 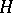passing through such that 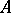is totally contained in one of the two half-spaces determined by 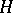. A support point 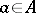is smooth (and called a smooth point of 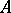) if there is only one closed hyperplane supporting at 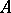. The set 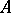is smooth if every boundary point is smooth. A space 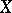is smooth, or smoothly normal, if the unit ball is smooth. Every separable Banach space can be smoothly renormed, i.e. there exists an equivalent smooth norm.

The dual property to "smooth" is strictly convex: Any non-identically zero continuous functional takes a maximum value on the closed unit ball at most at one point, or, equivalently, distinct boundary points of the closed unit ball have distinct supporting hyperplanes. For a linear normed space 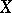one has that if the dual space 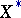is smooth (respectively, strictly convex), then 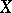is strictly convex (respectively, smooth).

References

[a1]	R.B. Holmes, "Geometric functional analysis and its applications" , Springer (1975)
[a2]	V. Barbu, Th. Precupanu, "Convexity and optimization in Banach spaces" , Reidel (1986)