Skolem-Mahler-Lech theorem

A recurrence sequence of order is a solution to a linear homogeneous recurrence relation with constant coefficients

Thus, the generating function of a recurrence is a rational function where , say; the polynomial of degree less than is determined by the initial values . If so, the distinct complex numbers 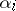are called the roots of the recurrence, and the 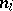their multiplicities. It follows that the are given by a generalized power sum (); the polynomial coefficients 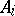are respectively of degree .

The theorem of Skolem–Mahler–Lech asserts that if a recurrence (equivalently, a generalized power sum) has infinitely many zeros, then those zeros occur periodically. That is, given a power series representing a rational function with infinitely many zero Taylor coefficients, the set is a finite union of complete arithmetic progressions (cf. Arithmetic progression), plus (a pre-period of) finitely many isolated zeros. By virtue of Ritt's quotient theorem [a6], it is equivalent that an infinitude of integer zeros of a complex exponential polynomial is accounted for by it being divisible (in the ring of exponential polynomials) by functions .

Skolem's argument was generalized by K. Mahler to algebraic number fields, and eventually to arbitrary fields of characteristic zero by C. Lech and by Mahler. The elegant argument of J.W.S. Cassels [a1] bypasses the technical complications in the chain of successive generalizations. In brief, one observes that there are rational primes 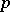so that (technically, after embedding the data in the field of 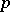-adic rationals) one has for each root. Then, for , each of the different 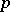-adic exponential polynomials is a -adic analytic function in the disc 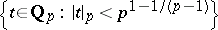. It follows that if any one of these functions has infinitely many zeros (it turns out, as few as zeros [a3]) in the unit disc, then it must vanish identically, yielding the theorem with arithmetic progressions with common difference . It follows that a recurrence sequence can have infinitely many zeros only if it is degenerate, that is, some quotient of its distinct roots is a root of unity.

The theorem is provable without visible appeal to 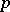-adic analysis [a2]. But a generalization, whereby if two recurrence sequences have infinitely many elements in common then they coincide along certain of their arithmetic subprogressions (see [a4]), as yet, (1996) relies on a 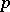-adic generalization of Schmidt's subspace theorem. A different generalization, Shapiro's conjecture, according to which two exponential polynomials with infinitely many complex common zeros must have a common exponential polynomial factor, is still (1996) mostly conjecture [a5].

A general reference surveying this and other relevant material is [a7].

References

[a1]	J.W.S. Cassels, "An embedding theorem for fields" Bull. Austral. Math. Soc. , 14 (1976) pp. 193–198 (Addendum: 14 (1976), 479–480)
[a2]	G. Hansel, "Une démonstration simple du théorème de Skolem–Mahler–Lech" Theor. Comput. Sci. , 43 (1986) pp. 91–98
[a3]	A.J. van der Poorten, R.S. Rumely, "Zeros of -adic exponential polynomials II" J. London Math. Soc. (2) , 36 (1987) pp. 1–15
[a4]	A.J. van der Poorten, H.-P. Schlickewei, "Additive relations in fields" J. Austral. Math. Soc. , 51 (1991) pp. 154–170
[a5]	A.J. van der Poorten, R. Tijdeman, "On common zeros of exponential polynomials" L'Enseign. Math. Série , 21 (1975) pp. 57–67
[a6]	J.F. Ritt, "On the zeros of exponential polynomials" Trans. Amer. Math. Soc. , 31 (1929) pp. 680–686
[a7]	A.J. van der Poorten, "Some facts that should be better known; especially about rational functions" R.A. Mollin (ed.) , Number Theory and Applications , NATO ASI , Kluwer Acad. Publ. (1989) pp. 497–528