Skew lines
Two straight lines in space that do not lie in a plane. The angle between two skew lines is defined as either of the angles between any two lines parallel to them and passing through a point of space. If  and
and 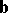 are the direction vectors of two skew lines, then the cosine of the angle between them is given by
are the direction vectors of two skew lines, then the cosine of the angle between them is given by
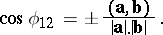 |
The common perpendicular of two skew lines is the line intersecting both of them at right angles. Any two skew lines have a unique common perpendicular. The equation (as the line of intersection of two planes) of this common perpendicular to the lines 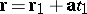 and
and 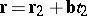 has the form
has the form
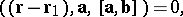 |
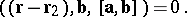 |
The distance between two skew lines is the length of the segment of their common perpendicular whose end points lie on the lines (or, the distance between the two parallel planes containing the two lines). The distance between two skew lines is given by
 |
Comments
References
| [a1] | D. Pedoe, "Geometry. A comprehensive introduction" , Dover, reprint (1988) |
Skew lines. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Skew_lines&oldid=15383