Singularity
of an analytic function
A set of singular points (cf. Singular point) of an analytic function 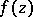 in the complex variables
in the complex variables  ,
, 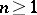 , defined by some supplementary conditions. In particular, isolated singular points (cf. Isolated singular point) are sometimes called isolated singularities.
, defined by some supplementary conditions. In particular, isolated singular points (cf. Isolated singular point) are sometimes called isolated singularities.
A set 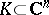 such that in a domain
such that in a domain 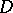 adjoining
adjoining 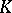 there is defined a single-valued analytic function
there is defined a single-valued analytic function  for which the question arises of the possibility of analytic continuation of
for which the question arises of the possibility of analytic continuation of 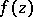 to
to  . For example, let
. For example, let 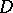 be a domain of the space
be a domain of the space 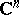 , let
, let 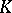 be a compactum contained in
be a compactum contained in 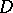 , and let
, and let 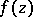 be holomorphic on
be holomorphic on 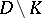 .
. 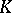 is then a possible singularity of
is then a possible singularity of 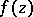 , and the question of analytic continuation (perhaps under certain supplementary conditions) of
, and the question of analytic continuation (perhaps under certain supplementary conditions) of 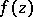 onto the entire domain
onto the entire domain 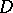 arises; in other words, the question of "elimination" or "removal" of the singularity
arises; in other words, the question of "elimination" or "removal" of the singularity 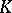 .
.
See also Removable set.
Comments
For references see also Singular point of an analytic function and Extension theorems (in analytic geometry). See also Hartogs theorem.
Singularity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Singularity&oldid=18225