Singular exponents
of a linear system of ordinary differential equations
The quantities defined by:
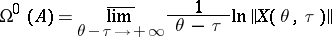 |
(the upper singular exponent) and
 |
(the lower singular exponent), where  is the Cauchy operator (i.e. the fundamental solution or principal solution) of the system
is the Cauchy operator (i.e. the fundamental solution or principal solution) of the system
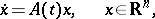 | (1) |
where 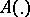 is a mapping
is a mapping 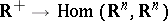 that is summable on every interval.
that is summable on every interval.
The singular exponents can be equal to 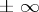 ; if for a certain
; if for a certain 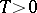 ,
,
 | (1prm) |
then the singular exponents are numbers.
For a system (1) with constant coefficients 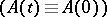 , the singular exponents
, the singular exponents 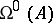 and
and  are equal to, respectively, the maximum and minimum of the real parts of the eigenvalues of the operator
are equal to, respectively, the maximum and minimum of the real parts of the eigenvalues of the operator 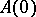 . For a system (1) with periodic coefficients (
. For a system (1) with periodic coefficients (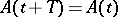 for all
for all 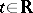 for a certain
for a certain 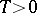 ), the singular exponents
), the singular exponents 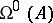 and
and 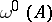 are equal to, respectively, the maximum and minimum of the logarithms of the absolute values of the multipliers, divided by the period
are equal to, respectively, the maximum and minimum of the logarithms of the absolute values of the multipliers, divided by the period 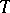 . The singular exponents are sometimes also called general exponents (see [4]).
. The singular exponents are sometimes also called general exponents (see [4]).
The following definitions are equivalent to those mentioned above if (1prm) holds for a certain 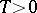 : The singular exponent
: The singular exponent 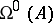 is equal to the greatest lower bound of the set of those numbers
is equal to the greatest lower bound of the set of those numbers 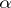 for each of which there is a number
for each of which there is a number  such that for any solution
such that for any solution 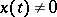 of the system (1) the inequality
of the system (1) the inequality
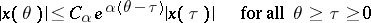 |
is fulfilled; the singular exponent 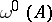 is equal to the least upper bound of the set of those numbers
is equal to the least upper bound of the set of those numbers 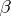 for each of which a number
for each of which a number 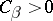 exists such that for every solution
exists such that for every solution 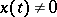 of the system (1) the inequality
of the system (1) the inequality
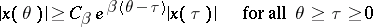 |
is fulfilled.
For the singular exponents and for the Lyapunov characteristic exponents (cf. Lyapunov characteristic exponent), for each 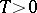 the inequalities
the inequalities
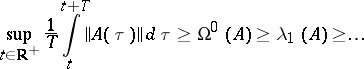 |
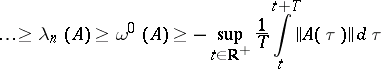 |
hold. For linear systems with constant or periodic coefficients,
 |
but there exist systems for which the corresponding inequalities are strict (see Uniform stability).
The singular exponent 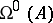 (respectively,
(respectively, 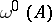 ), as a function on the space of all systems of the form (1) with bounded continuous coefficients (the mapping
), as a function on the space of all systems of the form (1) with bounded continuous coefficients (the mapping 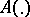 is continuous and
is continuous and 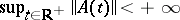 ) provided with the metric
) provided with the metric
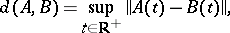 |
is semi-continuous from above (respectively, from below) but is not continuous everywhere.
If the mapping  is uniformly continuous and
is uniformly continuous and
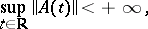 |
then the shift dynamical system 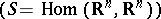 has invariant normalized measures
has invariant normalized measures 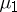 and
and 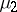 concentrated on the closure of the trajectory of the point
concentrated on the closure of the trajectory of the point 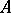 such that, for almost all
such that, for almost all 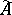 (in the sense of the measure
(in the sense of the measure 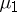 ), the upper singular exponent of the system
), the upper singular exponent of the system
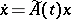 | (2) |
is equal to its largest (leading) Lyapunov characteristic exponent,
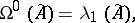 |
and for almost all 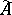 (in the sense of the measure
(in the sense of the measure 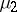 ), the lower singular exponent of the system (2) is equal to its smallest Lyapunov characteristic exponent,
), the lower singular exponent of the system (2) is equal to its smallest Lyapunov characteristic exponent,
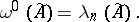 |
For almost-periodic mappings 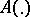 (see Linear system of differential equations with almost-periodic coefficients) the measures
(see Linear system of differential equations with almost-periodic coefficients) the measures 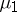 and
and 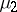 are identical and coincide with the unique normalized invariant measure concentrated on the restriction of the shift dynamical system to the closure of the trajectory of the point
are identical and coincide with the unique normalized invariant measure concentrated on the restriction of the shift dynamical system to the closure of the trajectory of the point  , which in this case exists.
, which in this case exists.
Let a dynamical system on a smooth, closed  -dimensional manifold
-dimensional manifold  be defined by a smooth vector field. Then there exist normalized invariant measures
be defined by a smooth vector field. Then there exist normalized invariant measures 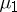 and
and 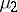 for this system such that for almost every point
for this system such that for almost every point 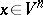 (in the sense of the measure
(in the sense of the measure  ) the upper singular exponent and the leading Lyapunov characteristic exponent of the system of variational equations (equations in variations, linearized equations) along the trajectory of the point
) the upper singular exponent and the leading Lyapunov characteristic exponent of the system of variational equations (equations in variations, linearized equations) along the trajectory of the point  coincide, and for almost every point
coincide, and for almost every point 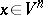 (in the sense of the measure
(in the sense of the measure 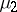 ) the lower singular exponent and the smallest Lyapunov characteristic exponent of the system of variational equations along the trajectory of the point
) the lower singular exponent and the smallest Lyapunov characteristic exponent of the system of variational equations along the trajectory of the point  coincide. The definitions of singular exponents, Lyapunov characteristic exponents, etc., retain their meaning for systems of variational equations of smooth dynamical systems defined on arbitrary smooth manifolds. The system of variational equations of such a dynamical system along the trajectory of a point
coincide. The definitions of singular exponents, Lyapunov characteristic exponents, etc., retain their meaning for systems of variational equations of smooth dynamical systems defined on arbitrary smooth manifolds. The system of variational equations of such a dynamical system along the trajectory of a point  can be written in the form (1) by using, for example, that basis in the tangent space to
can be written in the form (1) by using, for example, that basis in the tangent space to 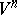 at every point of the trajectory of
at every point of the trajectory of  which is obtained by a parallel transfer along this trajectory (in the sense of the Riemannian connection induced by the smooth Riemannian metric) of some basis of the tangent space of
which is obtained by a parallel transfer along this trajectory (in the sense of the Riemannian connection induced by the smooth Riemannian metric) of some basis of the tangent space of 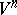 at
at  .
.
References
| [1] | P. Bohl, "Ueber Differentialgleichungen" J. Reine Angew. Math. , 144 (1913) pp. 284–318 |
| [2] | K. Persidskii, "First approximation kinetic stability" Mat. Sb. , 40 : 3 (1933) pp. 284–293 (In Russian) |
| [3] | B.F. Bylov, R.E. Vinograd, D.M. Grobman, V.V. Nemytskii, "The theory of Lyapunov exponents and its applications to problems of stability" , Moscow (1966) (In Russian) |
| [4] | Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [5] | N.A. Izobov, "Linear systems of ordinary differential equations" J. Soviet Math. , 5 : 1 (1974) pp. 46–96 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 71–146 |
Singular exponents. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Singular_exponents&oldid=11292