Singular distribution

A probability distribution on concentrated on a set of Lebesgue measure zero and giving probability zero to every one-point set.

On the real line 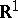, the definition of a singular distribution is equivalent to the following: A distribution is singular if the corresponding distribution function is continuous and its set of growth points has Lebesgue measure zero.

An example of a singular distribution on is a distribution concentrated on the Cantor set, the so-called Cantor distribution, which can be described in the following way. Let be a sequence of independent random variables, each of which takes on the values 0 and 1 with probability . Then the random variable

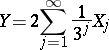has a Cantor distribution, and its characteristic function is equal to

An example of a singular distribution on 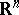(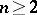) is a uniform distribution on a sphere of positive radius.

The convolution of two singular distributions can be singular, absolutely continuous or a mixture of the two.

Any probability distribution can be uniquely represented in the form

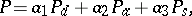where is discrete, is absolutely continuous, is singular, , and (Lebesgue decomposition).

Sometimes, singularity is understood in a wider sense: A probability distribution is singular with respect to a measure if it is concentrated on a set with 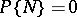. Under this definition, every discrete distribution is singular with respect to Lebesgue measure.

For singular set functions, see also Absolute continuity of set functions.

References

[1]	Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian)
[2]	W. Feller, "An introduction to probability theory and its applications" , 2 , Wiley (1971)