Sine-Gordon equation
A relativistically-invariant equation in two space-time variables, of the form
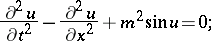 | (1) |
 |
The name was suggested by M. Kruskal, in analogy with the linear Klein–Gordon equation (where  appears in place of
appears in place of  ). In characteristic (light-cone) variables the sine-Gordon equation has the form
). In characteristic (light-cone) variables the sine-Gordon equation has the form
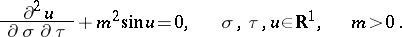 | (2) |
In both cases (1) and (2), the sine-Gordon equation admits a Lax representation
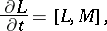 |
where  and
and  are linear operators and
are linear operators and  . This enables one to obtain solutions of the Cauchy problem by using the inverse scattering method.
. This enables one to obtain solutions of the Cauchy problem by using the inverse scattering method.
The Cauchy problem for the sine-Gordon equation is formulated in the following way.
Case (1):
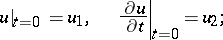 |
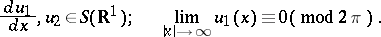 |
Case (2):
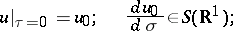 |
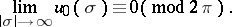 |
Here 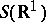 is the Schwartz space of rapidly-decreasing functions. Under certain additional restrictions on the initial conditions, the Cauchy problems (1) and (2) can be solved uniquely, and their solution sets coincide. The evolution of the scattering data for the corresponding
is the Schwartz space of rapidly-decreasing functions. Under certain additional restrictions on the initial conditions, the Cauchy problems (1) and (2) can be solved uniquely, and their solution sets coincide. The evolution of the scattering data for the corresponding 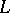 -operators is given by explicit formulas, and solutions
-operators is given by explicit formulas, and solutions 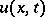 and
and 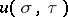 can be found by using integral equations of Gel'fand–Levitan–Marchenko type.
can be found by using integral equations of Gel'fand–Levitan–Marchenko type.
The periodic problem for the sine-Gordon equation can be studied by means of an algebraic-geometric method (similar to the case of the Korteweg–de Vries equation). In particular, one obtains explicit expressions for the finite-gap solutions of the sine-Gordon equation in terms of 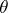 -functions on the corresponding Abelian varieties.
-functions on the corresponding Abelian varieties.
The Hamiltonian version of the sine-Gordon equation (in case (1), for example) is the Hamiltonian system with Hamiltonian
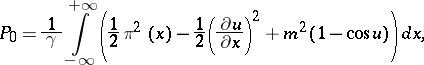 |
 |
and symplectic form
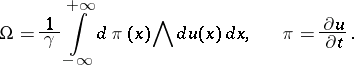 |
This system is completely integrable, and replacing the variables  and
and  by the scattering data of the corresponding operator
by the scattering data of the corresponding operator 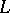 yields a canonical transformation into variables of action-angle type. The phase space is parametrized by canonically adjoint variables of three types:
yields a canonical transformation into variables of action-angle type. The phase space is parametrized by canonically adjoint variables of three types:
1) 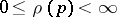 ,
, 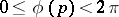 ,
, 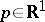 ;
;
2)  ,
,  ,
,  ,
, 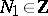 ;
;
3) 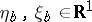 ,
, 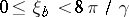 ,
, 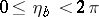 ,
, 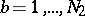 ,
, 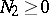 ,
, 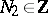 .
.
The total energy 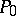 and total momentum
and total momentum
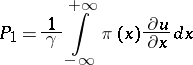 |
of the field  in terms of the new variables are as follows:
in terms of the new variables are as follows:
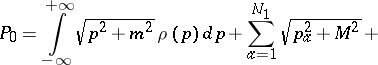 |
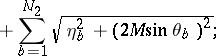 |
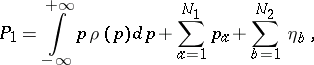 |
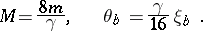 |
In case (1) one also obtains a completely-integrable Hamiltonian system.
An application to quantum field theory.
Let 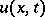 be a scalar field with Lagrangian
be a scalar field with Lagrangian
 |
where 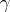 is the constant of interaction. The sine-Gordon equation is the Euler–Lagrange equation for this Lagrangian. In the quasi-classical quantization of the field
is the constant of interaction. The sine-Gordon equation is the Euler–Lagrange equation for this Lagrangian. In the quasi-classical quantization of the field  , a fundamental role is played by the above formulas for
, a fundamental role is played by the above formulas for 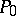 and
and 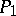 . The first terms on their right-hand sides correspond to particles of mass
. The first terms on their right-hand sides correspond to particles of mass 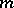 and to particles of the ground field, respectively (cf. also Soliton). The second and third terms correspond to localized solutions of the sine-Gordon equation, namely solitons and dual solitons with masses
and to particles of the ground field, respectively (cf. also Soliton). The second and third terms correspond to localized solutions of the sine-Gordon equation, namely solitons and dual solitons with masses 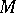 and
and 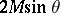 , respectively. The system obeys the conservation law (of topological charge):
, respectively. The system obeys the conservation law (of topological charge):
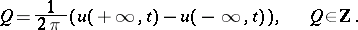 |
Particles of the first and third types have charge 0, while those of the second type have charge  . Particles with equal charges repulse, while those with different charges attract. The presence of infinitely-many conservation laws means that the number of particles of each type is preserved under scattering; the
. Particles with equal charges repulse, while those with different charges attract. The presence of infinitely-many conservation laws means that the number of particles of each type is preserved under scattering; the  -particle
-particle 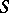 -matrix reduces to paired
-matrix reduces to paired 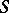 -matrices (cf. Scattering matrix). Using integrals over trajectories (cf. Integral over trajectories), one can compute the quantum corrections to the masses and to the quasi-classical
-matrices (cf. Scattering matrix). Using integrals over trajectories (cf. Integral over trajectories), one can compute the quantum corrections to the masses and to the quasi-classical 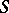 -matrix of solitons. One of the non-trivial properties of the above model is the appearance of a whole spectrum of particles (solitons), while the Lagrangian of the theory contains only one field. Furthermore, in the weak interaction approximation (that is, when
-matrix of solitons. One of the non-trivial properties of the above model is the appearance of a whole spectrum of particles (solitons), while the Lagrangian of the theory contains only one field. Furthermore, in the weak interaction approximation (that is, when 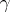 is small), solitons are heavy particles and interact strongly.
is small), solitons are heavy particles and interact strongly.
References
| [1] | M., et al. Ablowitz, "Method for solving the sine-Gordon equation" Phys. Rev. Letters , 30 (1973) pp. 1262–1264 |
| [2] | L.A. Takhtadzhyan, L.D. Faddeev, "Essentially nonlinear one-dimensional model of classical field theory" Teoret. Mat. Fiz. , 21 : 2 (1974) pp. 160–174 (In Russian) |
| [3] | L.A. [L.A. Takhtadzhyan] Tahtadžjan, L.D. Faddeev, "The Hamiltonian system connected with the equation 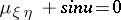 " Proc. Steklov Inst. Math. , 142 (1979) pp. 277–289 Trudy Mat. Inst. Akad. Nauk SSSR , 142 (1976) pp. 254–266 " Proc. Steklov Inst. Math. , 142 (1979) pp. 277–289 Trudy Mat. Inst. Akad. Nauk SSSR , 142 (1976) pp. 254–266 |
| [4] | V.O. Kozel, V.P. Kotlyarov, "Almost-periodic solutions of the equation 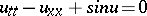 " Dokl. Akad. Nauk UkrSSR Ser. A , 10 (1976) pp. 878–881; 959 (In Russian) (English abstract) " Dokl. Akad. Nauk UkrSSR Ser. A , 10 (1976) pp. 878–881; 959 (In Russian) (English abstract) |
| [5] | V.E. Korepin, L.D. Faddeev, "Quantization of solitons" Teoret. Mat. Fiz. , 25 : 2 (1975) pp. 147–163 (In Russian) (English abstract) |
| [6] | L. Bianchi, "Lezioni di geometria differenziale" , 1–2 , Zanichelli , Bologna (1923–1927) |
| [7] | S.P. Finikov, "Deformation over a principal base and related problems in geometry" , Moscow-Leningrad (1937) (In Russian) |
| [8] | E.N. Pelinovskii, "Some exact methods in nonlinear wave theory" Izv. Vuzov. Radiofizika , 19 : 5–6 (1976) pp. 883–901 (In Russian) |
Comments
There are "canonical" sine-Gordon type equations associated to every Kac–Moody algebra [a5], [a4]. These are called Leznov–Saveliev systems. There are also Korteweg–de Vries type soliton equations associated to every Kac–Moody algebra, as well as modified Korteweg–de Vries type equations. These mKdV equations and Leznov–Saveliev systems associated to the same (extended) root system are "in duality" , in the sense that the solutions of the one serve as symmetries of the other and vice versa, [a4].
References
| [a1] | M.J. Ablowitz, H. Segur, "Solitons and the inverse scattering transform" , SIAM (1981) |
| [a2] | L.D. Faddeev, L.A. Takhtadzhyan, "Hamiltonian methods in the theory of solitons" , Springer (1967) (Translated from Russian) |
| [a3] | A.C. Newell, "Solitons in mathematics and physics" , SIAM (1985) |
| [a4] | V.G. Drinfel'd, V.V. Sokolov, "Lie algebras and equations of Korteweg–de Vries type" J. Soviet Math. , 30 (1985) pp. 1975–2005 Itogi Nauk. i Tekhn. Sovrem. Probl. Mat. , 24 (1984) pp. 81–180 |
| [a5] | A.N. Leznov, "On complete integrability of a nonlinear system of partial differential equations in two-dimensional space" Teoret. Mat. Fiz. , 42 : 3 (1980) pp. 343–349 (In Russian) |
Sine-Gordon equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sine-Gordon_equation&oldid=18822