Simply-connected domain
in a path-connected space
A domain  in which all closed paths are homotopic to zero, or, in other words, a domain whose fundamental group is trivial. This means that any closed path in
in which all closed paths are homotopic to zero, or, in other words, a domain whose fundamental group is trivial. This means that any closed path in  can be continuously deformed into a point, remaining the whole time in the simply-connected domain
can be continuously deformed into a point, remaining the whole time in the simply-connected domain  . The boundary of a simply-connected domain
. The boundary of a simply-connected domain  may, in general, consist of an arbitrary number
may, in general, consist of an arbitrary number  ,
,  , of connected components, even in the case of simply-connected domains in Euclidean spaces
, of connected components, even in the case of simply-connected domains in Euclidean spaces  ,
,  , or
, or  ,
,  . The boundary of a bounded planar simply-connected domain consists of a single connected component; all planar simply-connected domains are homeomorphic to each other.
. The boundary of a bounded planar simply-connected domain consists of a single connected component; all planar simply-connected domains are homeomorphic to each other.
See also Limit elements.
Comments
More generally, a simply-connected space  is a path-connected space for which each loop is contractible, i.e. whose fundamental group
is a path-connected space for which each loop is contractible, i.e. whose fundamental group 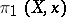 is zero for some (and hence all) base points
is zero for some (and hence all) base points  . The spheres
. The spheres  ,
, 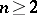 , are simply connected, but the two-dimensional torus and an annulus in
, are simply connected, but the two-dimensional torus and an annulus in 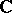 are not simply connected.
are not simply connected.
References
| [a1] | K. Jänich, "Topology" , Springer (1984) pp. 148ff (Translated from German) |
| [a2] | Z. Nehari, "Conformal mapping" , Dover, reprint (1975) pp. 2 |
Simply-connected domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Simply-connected_domain&oldid=14141