Simple ring

A ring, containing more than one element, without two-sided ideals (cf. Ideal) different from 0 and the entire ring. An associative simple ring with an identity element and containing a minimal one-sided ideal is isomorphic to a matrix ring over a some skew-field (cf. also Associative rings and algebras). Without the assumption on the existence of an identity, such a ring is locally matrix over some skew-field 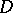, i.e. each of its finite subsets is contained in a subring isomorphic to a matrix ring over 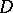(cf. [2]). There are simple rings without zero divisors (even Noetherian simple rings, cf. also Noetherian ring) different from a skew-field, as well as Noetherian simple rings with zero divisors but without idempotents [3]. Simple rings that are radical in the sense of N. Jacobson are known (cf. [1]). However, the problem of the existence of simple nil rings remains open.

The description of the structure of alternative simple rings reduces to the associative case (cf. Alternative rings and algebras). See also Simple algebra.

References

[1]	L.A. Bokut', "Associative rings" , 1–2 , Novosibirsk (1977–1981) (In Russian)
[2]	N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956)
[3]	A.E. Zalesskii, O. Neroslavskii, "There exist simple Noetherian rings with zero division but without idempotents" Comm. in Algebra , 5 : 3 (1977) pp. 231–244 (In Russian) (English abstract)
[4]	C. Faith, "Algebra" , 1–2 , Springer (1973–1976)
[5]	J. Cozzens, C. Faith, "Simple Noetherian rings" , Cambridge Univ. Press (1975)