Difference between revisions of "Simple-layer potential"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48703 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
An expression | An expression | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s0852601.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s0852602.png" /> is a closed Lyapunov surface (of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s0852603.png" />, cf. [[Lyapunov surfaces and curves|Lyapunov surfaces and curves]]) in the Euclidean space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s0852604.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s0852605.png" />, separating <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s0852606.png" /> into an interior domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s0852607.png" /> and an exterior domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s0852608.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s0852609.png" /> is a [[Fundamental solution|fundamental solution]] of the [[Laplace operator|Laplace operator]]: | |
| − | |||
| − | a | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526010.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526011.png" /> is the area of the unit sphere in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526012.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526013.png" /> is the distance between two points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526014.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526015.png" />; and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526016.png" /> is the area element on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526017.png" />. | |
| − | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526018.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526019.png" /> is everywhere defined on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526020.png" />. A simple-layer potential is a particular case of a [[Newton potential|Newton potential]], generated by masses distributed on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526021.png" /> with surface density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526022.png" />, and with the following properties. | |
| − | + | In <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526024.png" /> a simple-layer potential <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526025.png" /> has derivatives of all orders, which can be calculated by differentiation under the integral sign, and satisfies the [[Laplace equation|Laplace equation]], <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526026.png" />, i.e. it is a [[Harmonic function|harmonic function]]. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526027.png" /> it is a function regular at infinity, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526028.png" />. A simple-layer potential is continuous throughout <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526029.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526030.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526031.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526032.png" />. When passing through the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526033.png" />, the derivative along the outward normal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526034.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526035.png" /> at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526036.png" /> undergoes a discontinuity. The limit values of the normal derivative from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526037.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526038.png" /> exist, are everywhere continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526039.png" />, and can be expressed, respectively, by the formula: | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526040.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526041.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
where | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526042.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | is the so-called direct value of the normal derivative of a simple-layer potential at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526043.png" />. Moreover, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526044.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526045.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526046.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526047.png" />, then the partial derivatives of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526048.png" /> can be continuously extended to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526049.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526050.png" /> as functions of the classes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526051.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526052.png" />, respectively. In this case one also has | |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526053.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | These properties can be generalized in various directions. E.g., if | + | These properties can be generalized in various directions. E.g., if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526054.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526055.png" /> inside and on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526056.png" />, formulas (2) hold almost everywhere on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526057.png" />, and the integral in (3) is summable on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526058.png" />. One has also studied properties of simple-layer potentials understood as integrals with respect to arbitrary Radon measures <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526059.png" /> concentrated on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526060.png" />: |
| − | then | ||
| − | inside and on | ||
| − | formulas (2) hold almost everywhere on | ||
| − | and the integral in (3) is summable on | ||
| − | One has also studied properties of simple-layer potentials understood as integrals with respect to arbitrary Radon measures | ||
| − | concentrated on | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526061.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | Here, also, | + | Here, also, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526062.png" /> is a harmonic function outside <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526063.png" />, and formulas (2) hold almost everywhere on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526064.png" /> with respect to the Lebesgue measure, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526065.png" /> is replaced by the derivative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526066.png" /> of the measure. In definition (1) one can replace the fundamental solution of the Laplace equation by an arbitrary Lewy function of a general second-order elliptic operator with variable coefficients of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526067.png" />, replacing the normal derivative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526068.png" /> by the derivative along the co-normal. The properties listed remain true in this case (cf. [[#References|[2]]], [[#References|[3]]], [[#References|[4]]]). |
| − | is a harmonic function outside | ||
| − | and formulas (2) hold almost everywhere on | ||
| − | with respect to the Lebesgue measure, where | ||
| − | is replaced by the derivative | ||
| − | of the measure. In definition (1) one can replace the fundamental solution of the Laplace equation by an arbitrary Lewy function of a general second-order elliptic operator with variable coefficients of class | ||
| − | replacing the normal derivative | ||
| − | by the derivative along the co-normal. The properties listed remain true in this case (cf. [[#References|[2]]], [[#References|[3]]], [[#References|[4]]]). | ||
| − | Simple-layer potentials are used in solving boundary value problems for elliptic equations. The solution of a second boundary value problem with prescribed normal derivative is represented as a simple-layer potential with unknown density | + | Simple-layer potentials are used in solving boundary value problems for elliptic equations. The solution of a second boundary value problem with prescribed normal derivative is represented as a simple-layer potential with unknown density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526069.png" />; the use of (2) and (3) leads to a Fredholm integral equation of the second kind on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526070.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526071.png" /> (cf. [[#References|[2]]]–[[#References|[5]]]). |
| − | the use of (2) and (3) leads to a Fredholm integral equation of the second kind on | ||
| − | for | ||
| − | cf. [[#References|[2]]]–[[#References|[5]]]). | ||
In solving boundary value problems for parabolic equations one uses simple-layer heat potentials, of the form | In solving boundary value problems for parabolic equations one uses simple-layer heat potentials, of the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526072.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
where | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526073.png" /></td> </tr></table> | |
| − | |||
| − | + | is the fundamental solution of the heat equation in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526074.png" />-dimensional space, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526075.png" /> is the density. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526076.png" /> and its generalization to arbitrary second-order parabolic equations have properties analogous to those indicated for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526077.png" /> (cf. [[#References|[3]]], [[#References|[4]]], [[#References|[6]]]). | |
| − | + | ====References==== | |
| − | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.M. Günter, "Potential theory and its applications to basic problems of mathematical physics" , F. Ungar (1967) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.N. Tikhonov, A.A. Samarskii, "Equations of mathematical physics" , Pergamon (1963) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.I. Smirnov, "A course of higher mathematics" , '''4''' , Addison-Wesley (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A.V. Bitsadze, "Boundary value problems for second-order elliptic equations" , North-Holland (1968) (Translated from Russian)</TD></TR></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | See [[#References|[a1]]] for simple-layer potentials on more general open sets in | + | See [[#References|[a1]]] for simple-layer potentials on more general open sets in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085260/s08526078.png" />. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Král, "Integral operators in potential theory" , ''Lect. notes in math.'' , '''823''' , Springer (1980)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Král, "Integral operators in potential theory" , ''Lect. notes in math.'' , '''823''' , Springer (1980)</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
An expression
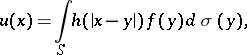 | (1) |
where 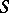 is a closed Lyapunov surface (of class
is a closed Lyapunov surface (of class  , cf. Lyapunov surfaces and curves) in the Euclidean space
, cf. Lyapunov surfaces and curves) in the Euclidean space 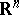 ,
,  , separating
, separating 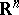 into an interior domain
into an interior domain 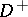 and an exterior domain
and an exterior domain 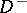 ;
; 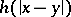 is a fundamental solution of the Laplace operator:
is a fundamental solution of the Laplace operator:
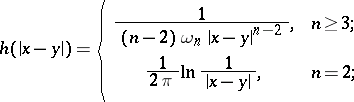 |
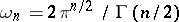 is the area of the unit sphere in
is the area of the unit sphere in 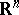 ;
; 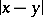 is the distance between two points
is the distance between two points  and
and 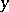 ; and
; and 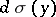 is the area element on
is the area element on 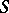 .
.
If  , then
, then  is everywhere defined on
is everywhere defined on 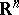 . A simple-layer potential is a particular case of a Newton potential, generated by masses distributed on
. A simple-layer potential is a particular case of a Newton potential, generated by masses distributed on 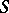 with surface density
with surface density 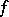 , and with the following properties.
, and with the following properties.
In 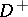 and
and 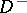 a simple-layer potential
a simple-layer potential  has derivatives of all orders, which can be calculated by differentiation under the integral sign, and satisfies the Laplace equation,
has derivatives of all orders, which can be calculated by differentiation under the integral sign, and satisfies the Laplace equation, 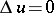 , i.e. it is a harmonic function. For
, i.e. it is a harmonic function. For 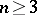 it is a function regular at infinity,
it is a function regular at infinity, 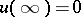 . A simple-layer potential is continuous throughout
. A simple-layer potential is continuous throughout 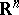 , and
, and 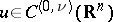 for any
for any  ,
, 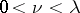 . When passing through the surface
. When passing through the surface 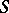 , the derivative along the outward normal
, the derivative along the outward normal 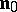 to
to 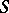 at a point
at a point 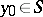 undergoes a discontinuity. The limit values of the normal derivative from
undergoes a discontinuity. The limit values of the normal derivative from 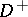 and
and  exist, are everywhere continuous on
exist, are everywhere continuous on 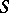 , and can be expressed, respectively, by the formula:
, and can be expressed, respectively, by the formula:
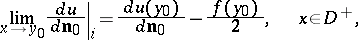 | (2) |
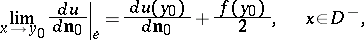 |
where
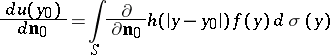 | (3) |
is the so-called direct value of the normal derivative of a simple-layer potential at a point 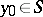 . Moreover,
. Moreover, 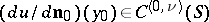 for all
for all  ,
, 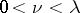 . If
. If 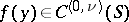 , then the partial derivatives of
, then the partial derivatives of 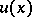 can be continuously extended to
can be continuously extended to 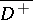 and
and 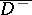 as functions of the classes
as functions of the classes 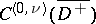 and
and 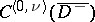 , respectively. In this case one also has
, respectively. In this case one also has
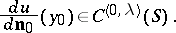 |
These properties can be generalized in various directions. E.g., if 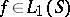 , then
, then 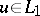 inside and on
inside and on 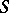 , formulas (2) hold almost everywhere on
, formulas (2) hold almost everywhere on 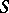 , and the integral in (3) is summable on
, and the integral in (3) is summable on 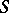 . One has also studied properties of simple-layer potentials understood as integrals with respect to arbitrary Radon measures
. One has also studied properties of simple-layer potentials understood as integrals with respect to arbitrary Radon measures  concentrated on
concentrated on 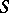 :
:
 |
Here, also,  is a harmonic function outside
is a harmonic function outside 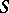 , and formulas (2) hold almost everywhere on
, and formulas (2) hold almost everywhere on 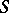 with respect to the Lebesgue measure, where
with respect to the Lebesgue measure, where 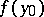 is replaced by the derivative
is replaced by the derivative 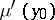 of the measure. In definition (1) one can replace the fundamental solution of the Laplace equation by an arbitrary Lewy function of a general second-order elliptic operator with variable coefficients of class
of the measure. In definition (1) one can replace the fundamental solution of the Laplace equation by an arbitrary Lewy function of a general second-order elliptic operator with variable coefficients of class 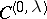 , replacing the normal derivative
, replacing the normal derivative 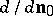 by the derivative along the co-normal. The properties listed remain true in this case (cf. [2], [3], [4]).
by the derivative along the co-normal. The properties listed remain true in this case (cf. [2], [3], [4]).
Simple-layer potentials are used in solving boundary value problems for elliptic equations. The solution of a second boundary value problem with prescribed normal derivative is represented as a simple-layer potential with unknown density 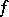 ; the use of (2) and (3) leads to a Fredholm integral equation of the second kind on
; the use of (2) and (3) leads to a Fredholm integral equation of the second kind on 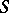 for
for 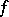 (cf. [2]–[5]).
(cf. [2]–[5]).
In solving boundary value problems for parabolic equations one uses simple-layer heat potentials, of the form
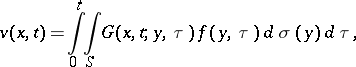 |
where
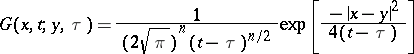 |
is the fundamental solution of the heat equation in the  -dimensional space, and
-dimensional space, and 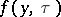 is the density. The function
is the density. The function  and its generalization to arbitrary second-order parabolic equations have properties analogous to those indicated for
and its generalization to arbitrary second-order parabolic equations have properties analogous to those indicated for  (cf. [3], [4], [6]).
(cf. [3], [4], [6]).
References
| [1] | N.M. Günter, "Potential theory and its applications to basic problems of mathematical physics" , F. Ungar (1967) (Translated from Russian) |
| [2] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
| [3] | A.N. Tikhonov, A.A. Samarskii, "Equations of mathematical physics" , Pergamon (1963) (Translated from Russian) |
| [4] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
| [5] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) |
| [6] | A.V. Bitsadze, "Boundary value problems for second-order elliptic equations" , North-Holland (1968) (Translated from Russian) |
Comments
See [a1] for simple-layer potentials on more general open sets in 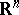 .
.
References
| [a1] | J. Král, "Integral operators in potential theory" , Lect. notes in math. , 823 , Springer (1980) |
Simple-layer potential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Simple-layer_potential&oldid=49425