Shooting method
A method for solving initial and boundary value problems for ordinary differential equations. It consists of introducing control variables (parameters) and subsequently determining them from the system of equations, where this choice of parameters has a decisive influence on the acceleration of the solution of the system.
Suppose, for 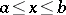 , one is given the differential equation
, one is given the differential equation
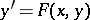 | (1) |
with boundary condition
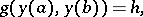 | (2) |
where the vector function 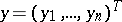 of
of  is to be determined, the vector functions
is to be determined, the vector functions 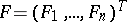 and
and 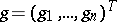 are known, and the numerical vector
are known, and the numerical vector 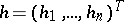 is given.
is given.
Suppose that the Cauchy problem
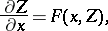 | (3) |
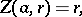 | (4) |
where 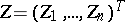 and
and  , has a unique solution
, has a unique solution 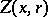 , defined for
, defined for 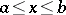 ,
, 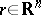 . Upon substituting in (2) for
. Upon substituting in (2) for 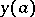 the given value
the given value 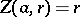 and for
and for 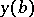 the calculated value
the calculated value 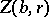 , one obtains the equation
, one obtains the equation
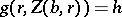 | (5) |
with respect to the parameter  .
.
The algorithm of the shooting method is as follows. First one finds a solution  of (5), and subsequently the required solution of the boundary value problem (1)–(2) as the solution of the Cauchy problem
of (5), and subsequently the required solution of the boundary value problem (1)–(2) as the solution of the Cauchy problem
 |
This problem can be solved using numerical methods. In order to solve (5) it is usually necessary to choose some iteration method.
If some of the components of 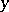 depend on
depend on 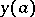 alone and the others on
alone and the others on 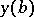 alone, it is useful to make another choice of parameters (cf. [1], as well as Non-linear boundary value problem, numerical methods). There are other versions of the shooting method (cf. [4]). The shooting method is also used in solving grid boundary value problems.
alone, it is useful to make another choice of parameters (cf. [1], as well as Non-linear boundary value problem, numerical methods). There are other versions of the shooting method (cf. [4]). The shooting method is also used in solving grid boundary value problems.
References
| [1] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
| [2] | S.K. Godunov, V.S. Ryaben'kii, "The theory of difference schemes" , North-Holland (1964) (Translated from Russian) |
| [3] | V.I. Krylov, V.V. Bobkov, P.I. Monastyrnyi, "Numerical methods" , 2 , Moscow (1977) (In Russian) |
| [4] | G. Hall (ed.) J.M. Watt (ed.) , Modern numerical methods for ordinary differential equations , Clarendon Press (1976) |
Comments
References
| [a1] | U.M. Ascher, R.M.M. Mattheij, R.D. Russell, "Numerical solution for boundary value problems for ordinary differential equations" , Prentice-Hall (1988) |
Shooting method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Shooting_method&oldid=11994