Shell theory
An area of elasticity theory (cf. Elasticity, mathematical theory of) and structural mechanics the main aim of which is to describe the stresses and deformations that arise from the action of external loadings on a shell. A shell is a solid body bounded by two surfaces, the thickness of which is small in comparison with its other typical dimensions. Other external effects are also considered in shell theory, for example, that of heat.
In shell theory one introduces a smooth surface 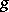 , called the mean surface, on each side of which the points of the bounding surfaces lie at a distance
, called the mean surface, on each side of which the points of the bounding surfaces lie at a distance 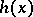 along the normals to
along the normals to 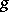 . In the majority of cases the thickness is constant:
. In the majority of cases the thickness is constant: 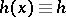 . The most widespread version of shell theory uses the so-called Kirchhoff–Love hypothesis, according to which every fibre normal to
. The most widespread version of shell theory uses the so-called Kirchhoff–Love hypothesis, according to which every fibre normal to 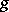 (a line segment perpendicular to the mean surface) remains straight after the deformation, and its length and perpendicularity to the mean surface are preserved. Under this assumption the system of equations of three-dimensional elasticity theory describing the displacement of the points of the shell as an elastic solid body reduces to a system of three differential equations in two independent variables
(a line segment perpendicular to the mean surface) remains straight after the deformation, and its length and perpendicularity to the mean surface are preserved. Under this assumption the system of equations of three-dimensional elasticity theory describing the displacement of the points of the shell as an elastic solid body reduces to a system of three differential equations in two independent variables 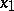 and
and 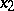 — the curvilinear coordinates of the point
— the curvilinear coordinates of the point  in the undeformed mean surface
in the undeformed mean surface 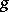 . In general this system is non-linear. Under additional assumptions about the smallness of the deformations and the external loadings the non-linear terms may be neglected. The problem reduces to the solution of the linear system
. In general this system is non-linear. Under additional assumptions about the smallness of the deformations and the external loadings the non-linear terms may be neglected. The problem reduces to the solution of the linear system
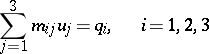 | (1) |
(see [3], [4]), in which 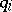 are the components of the external loading,
are the components of the external loading, 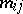 are linear differential operators with coefficients depending on the geometrical characteristics of the surface
are linear differential operators with coefficients depending on the geometrical characteristics of the surface 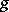 , and
, and 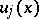 are the desired components of the displacement vector of a point on the mean surface. The system (1) is solved under four boundary conditions, which depend on the way in which the boundary of
are the desired components of the displacement vector of a point on the mean surface. The system (1) is solved under four boundary conditions, which depend on the way in which the boundary of 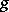 is fixed. The operators
is fixed. The operators 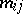 in (1) have the special form
in (1) have the special form
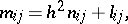 |
where a small parameter  stands in front of the leading derivatives. The system (1) is elliptic in the sense of Douglis and Nirenberg (see [5]) and formally self-adjoint (see [7]). Under naturally arising boundary conditions, (1) gives rise to an elliptic boundary value problem. The system (1) is conveniently called the system of equations of moment shell theory, since its derivation takes into account terms containing bending moments and torques. Under additional assumptions these terms can be neglected, leading to moment-free (membrane) shell theory. Formally, this corresponds to removing the terms in (1) containing the small parameter
stands in front of the leading derivatives. The system (1) is elliptic in the sense of Douglis and Nirenberg (see [5]) and formally self-adjoint (see [7]). Under naturally arising boundary conditions, (1) gives rise to an elliptic boundary value problem. The system (1) is conveniently called the system of equations of moment shell theory, since its derivation takes into account terms containing bending moments and torques. Under additional assumptions these terms can be neglected, leading to moment-free (membrane) shell theory. Formally, this corresponds to removing the terms in (1) containing the small parameter 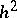 . The moment-free system
. The moment-free system
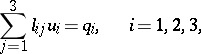 | (2) |
is essentially simpler than (1). The operators in (2) are of at most second order. The order of the determinant of the principal symbol (characteristic polynomial) in (2) is 4, while in (1) it is 8.
The presence of a small parameter in (1) allows one to use a procedure of asymptotic integration (see [4]). If the Gaussian curvature 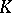 of the mean surface
of the mean surface 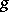 is positive, (2) is an elliptic system and under conditions of a complete or partial fixation of the boundary, the degeneration of the moment problem to the moment-free problem as
is positive, (2) is an elliptic system and under conditions of a complete or partial fixation of the boundary, the degeneration of the moment problem to the moment-free problem as 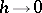 is regular. A significant divergence of the solutions is possible only in a small neighbourhood of the boundary of
is regular. A significant divergence of the solutions is possible only in a small neighbourhood of the boundary of 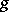 (a boundary effect). For
(a boundary effect). For 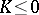 the picture of degeneration of the moment system as
the picture of degeneration of the moment system as 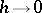 is essentially more complicated; the passage from system (1) to (2) may lead to significant errors not only on the boundary of
is essentially more complicated; the passage from system (1) to (2) may lead to significant errors not only on the boundary of 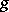 , but also everywhere inside. The procedure of asymptotic integration used in shell theory for non-regular degeneration has not yet (1990) found mathematical justification.
, but also everywhere inside. The procedure of asymptotic integration used in shell theory for non-regular degeneration has not yet (1990) found mathematical justification.
Moment-free shell theory is closely related to the problem of infinitesimal deformation of surfaces. The introduction of the technique of generalized analytic functions (cf. Generalized analytic function, see [2]) made a significant contribution both to moment-free shell theory and to the theory of infinitesimal deformation.
An important problem in shell theory is the investigation of the stability of the equilibrium form, and the related problem of determining the critical loading. These problems can be considered in linear (more precisely, linearized) and non-linear formulations. One of the methods for solving them in the non-linear formulation makes essential use of deformation theory (see [8]).
In statical problems an effective method is that of complex representation of the equations of shell theory, enabling one to reduce the system (1) by means of auxiliary functions to an equivalent system with a characteristic polynomial of degree 4 (see [7]).
Among the problems of dynamics undergoing intensive mathematical analysis is the problem of free and forced vibrations of a shell. The structure of the spectrum of fundamental frequencies and the construction of the corresponding forms of free vibration have been found by methods of asymptotic integration and by the spectral theory of operators (see [5], [9]).
Methods of numerical mathematics have been extensively used in shell theory. For the case of separable variables in statical and dynamical problems the shooting method is particularly effective, while for shells of arbitrary shape, the finite-element method is appropriate.
References
| [1] | N.A. Alumyae, "Theory of elastic shells and plates" , Mechanics in the USSR during 50 years , 3 , Moscow (1972) pp. 227–266 (In Russian) |
| [2] | I.N. Vekua, "Generalized analytic functions" , Pergamon (1962) (Translated from Russian) |
| [3] | W.S. [V.Z. Vlasov] Wlassow, "Allgemeine Schalentheorie und ihre Anwendung in der Technik" , Akademie Verlag (1958) (Translated from Russian) |
| [4] | A.L. Gol'denveizer, "The theory of thin elastic shells" , Pergamon (1961) (In Russian) |
| [5] | A.L. Gol'denveizer, V.B. Lidskii, P.E. Tovstik, "Free vibrations of thin elastic shells" , Moscow (1979) (In Russian) |
| [6] | Kh.M. Mushtari, K. Galimov, "The non-linear theory of elastic shells" , Israel Program Sci. Transl. (1961) (Translated from Russian) |
| [7] | V.V. Novozhilov, "The theory of thin shells" , Noordhoff (1959) (Translated from Russian) |
| [8] | A.V. Pogorelov, "Geometric methods in the non-linear theory of elastic shells" , Moscow (1967) (In Russian) |
| [9] | , Strength. Stability. Vibrations. A handbook , 3 , Moscow (1968) (In Russian) |
Comments
In most cases of practical interest it is not possible to remove the terms 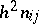 completely (e.g. in the case of the bending of a circular cylinder).
completely (e.g. in the case of the bending of a circular cylinder).
References
| [a1] | W. Flügge, "Stresses in shells" , Springer (1967) (Translated from German) |
| [a2] | S.P. Timoshenko, S. Woinowsky-Krieger, "Theory of plates and shells" , McGraw-Hill (1959) |
Shell theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Shell_theory&oldid=16695