Sheaf theory
A special mathematical tool which provides a unified approach to establishing connections between local and global properties of topological spaces (in particular geometric objects) and which is a powerful method for studying many problems in contemporary algebra, geometry, topology, and analysis.
A pre-sheaf 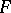 on a topological space
on a topological space 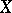 assigns to each open subset
assigns to each open subset 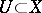 an Abelian group
an Abelian group 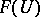 (a ring, a module over a ring, etc.) and to every pair of open sets
(a ring, a module over a ring, etc.) and to every pair of open sets 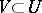 a homomorphism
a homomorphism 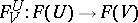 , such that
, such that 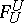 is the identity isomorphism and
is the identity isomorphism and 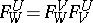 for every triple
for every triple 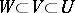 . In other words, a pre-sheaf is a contravariant functor from the category of open subsets of
. In other words, a pre-sheaf is a contravariant functor from the category of open subsets of 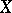 and their inclusions into the category of groups (rings, etc.) and their homomorphisms. The mappings
and their inclusions into the category of groups (rings, etc.) and their homomorphisms. The mappings 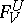 are called restriction homomorphisms (for example, if the elements of the stalk
are called restriction homomorphisms (for example, if the elements of the stalk 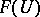 are functions of some type or other defined on
are functions of some type or other defined on 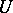 ,
, 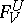 is the restriction of these to the smaller subset). A topology on the set
is the restriction of these to the smaller subset). A topology on the set 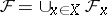 , where
, where 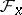 is, by definition, the direct limit
is, by definition, the direct limit 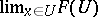 , is defined in the following way: For each
, is defined in the following way: For each 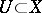 and any
and any 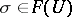 , the set
, the set 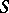 consisting of those points of
consisting of those points of 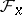 ,
, 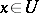 , which are images of
, which are images of  in the definition of
in the definition of  is declared to be open in
is declared to be open in 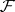 . In this topology the stalks
. In this topology the stalks 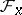 are discrete, the stalk-wise algebraic operations defined on
are discrete, the stalk-wise algebraic operations defined on 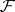 by taking direct limits are continuous and the natural projection
by taking direct limits are continuous and the natural projection  , where
, where 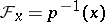 , is a local homeomorphism. The space
, is a local homeomorphism. The space 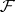 together with the stalk-wise algebraic operations and the projection
together with the stalk-wise algebraic operations and the projection 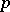 is called the sheaf of Abelian groups (rings, etc.) over
is called the sheaf of Abelian groups (rings, etc.) over 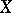 associated with the pre-sheaf
associated with the pre-sheaf  .
.
Every continuous mapping 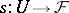 for which
for which 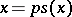 is called a section of
is called a section of 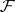 over
over  . The section of
. The section of 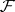 over
over 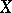 defined by the zeros in
defined by the zeros in 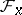 is called the zero section. If a section
is called the zero section. If a section  is zero at a point
is zero at a point  , then
, then  coincides with the zero section in some neighbourhood of
coincides with the zero section in some neighbourhood of  ; therefore the set of points at which
; therefore the set of points at which  is not zero (the support of
is not zero (the support of  ) is closed in
) is closed in 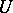 .
.
Let 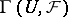 (respectively,
(respectively, 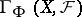 , where
, where 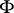 is a certain family of closed sets in
is a certain family of closed sets in  ; in particular,
; in particular, 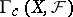 ) be the group (ring, module, etc.) of all sections of
) be the group (ring, module, etc.) of all sections of 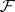 over
over 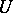 (respectively, all sections over
(respectively, all sections over  with supports in
with supports in 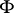 ; in particular, sections with compact support). The assignment
; in particular, sections with compact support). The assignment 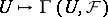 is a pre-sheaf over
is a pre-sheaf over 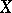 , called the pre-sheaf of sections of the sheaf
, called the pre-sheaf of sections of the sheaf 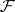 . The assignment
. The assignment 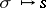 used in defining the topology on
used in defining the topology on  also defines homomorphisms
also defines homomorphisms 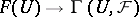 which commute with the restrictions to
which commute with the restrictions to 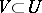 , that is, it defines a homomorphism of pre-sheaves. This homomorphism is an isomorphism provided that the original pre-sheaf
, that is, it defines a homomorphism of pre-sheaves. This homomorphism is an isomorphism provided that the original pre-sheaf 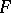 satisfies the requirements: a) if
satisfies the requirements: a) if 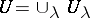 and
and 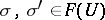 , then
, then 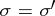 if the restrictions of
if the restrictions of 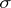 and
and 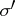 to each
to each 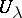 are equal; and b) if
are equal; and b) if 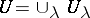 and
and 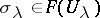 is a collection of elements such that the restrictions of
is a collection of elements such that the restrictions of 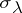 and
and 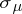 to
to 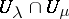 coincide, then there exists a
coincide, then there exists a 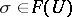 which has restriction to each
which has restriction to each 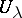 coinciding with
coinciding with 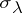 . The concept of a pre-sheaf satisfying these requirements is equivalent to the concept of the sheaf associated with it, therefore such pre-sheaves are quite often called sheaves also.
. The concept of a pre-sheaf satisfying these requirements is equivalent to the concept of the sheaf associated with it, therefore such pre-sheaves are quite often called sheaves also.
A sheaf of the form 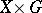 (with the evident projection to
(with the evident projection to 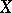 ), where
), where 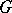 is a fixed group (ring, etc.), is called a constant sheaf, and is denoted by
is a fixed group (ring, etc.), is called a constant sheaf, and is denoted by 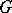 . A sheaf which is constant in sufficiently small neighbourhoods of every
. A sheaf which is constant in sufficiently small neighbourhoods of every 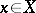 is called locally constant. The topology of such sheaves is separated (i.e. Hausdorff) if
is called locally constant. The topology of such sheaves is separated (i.e. Hausdorff) if 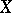 is a separated space. In more typical situations the topology of
is a separated space. In more typical situations the topology of 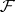 can be non-separated even if
can be non-separated even if 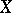 is separated (such is the case, for example, for the sheaf of germs of continuous (or differentiable) functions which is generated by the pre-sheaf
is separated (such is the case, for example, for the sheaf of germs of continuous (or differentiable) functions which is generated by the pre-sheaf 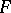 , where
, where 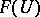 is the set of continuous (differentiable) functions on
is the set of continuous (differentiable) functions on 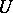 ; however, the sheaf of germs of analytic functions on a manifold is separated).
; however, the sheaf of germs of analytic functions on a manifold is separated).
Every homomorphism of pre-sheaves 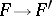 induces a mapping of the associated sheaves
induces a mapping of the associated sheaves 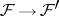 , which is a local homeomorphism and maps stalks homomorphically to stalks; such a mapping of sheaves is called a sheaf homomorphism. Mono- and epimorphisms are defined in the standard way. For any sheaf homomorphism
, which is a local homeomorphism and maps stalks homomorphically to stalks; such a mapping of sheaves is called a sheaf homomorphism. Mono- and epimorphisms are defined in the standard way. For any sheaf homomorphism 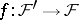 the image
the image 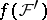 is an open subset of
is an open subset of 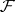 , closed with respect to the stalk-wise algebraic operations. Every subset of
, closed with respect to the stalk-wise algebraic operations. Every subset of  which satisfies these requirements is called a subsheaf of
which satisfies these requirements is called a subsheaf of 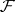 . The quotient sheaf of the sheaf
. The quotient sheaf of the sheaf 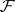 by a subsheaf
by a subsheaf 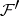 is defined as the sheaf
is defined as the sheaf 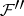 associated with the pre-sheaf
associated with the pre-sheaf 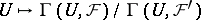 ; moreover, there is an epimorphism
; moreover, there is an epimorphism  , and
, and 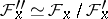 . For every open
. For every open 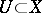 there is a subsheaf in
there is a subsheaf in 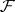 , denoted by
, denoted by 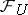 , which is the union of
, which is the union of 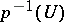 with the zero section of
with the zero section of 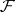 over
over 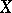 ;
; 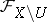 denotes the corresponding quotient sheaf (whose restriction to
denotes the corresponding quotient sheaf (whose restriction to 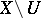 coincides with the restriction thereto of
coincides with the restriction thereto of 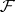 ).
).
Since it is possible to interpret such ordinary terms as homomorphism, kernel, image, subsheaf, quotient sheaf, etc. for sheaves over 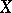 in such a way that these concepts have essentially the same meaning as in algebra, one can consider them from a categorical point of view and apply to sheaf theory the constructions of homological algebra. The resulting category of sheaves over
in such a way that these concepts have essentially the same meaning as in algebra, one can consider them from a categorical point of view and apply to sheaf theory the constructions of homological algebra. The resulting category of sheaves over 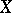 has the same classical properties as the category of Abelian groups or the category of modules; in particular, one can define for sheaves direct sums, infinite direct products, inductive limits, and other concepts.
has the same classical properties as the category of Abelian groups or the category of modules; in particular, one can define for sheaves direct sums, infinite direct products, inductive limits, and other concepts.
The apparatus of sheaf theory has penetrated into various fields of mathematics thanks to the fact that there is a natural definition of the cohomology 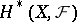 of a space
of a space 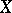 with coefficients in a sheaf
with coefficients in a sheaf 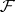 , and this without any kind of restrictions on
, and this without any kind of restrictions on 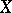 (this is essential, for example, in algebraic geometry, where the spaces arising are, as a rule, non-separated) and to the fact that other cohomologies (under certain specific conditions) reduce to a sheaf cohomology, at least in those situations where their application is justified.
(this is essential, for example, in algebraic geometry, where the spaces arising are, as a rule, non-separated) and to the fact that other cohomologies (under certain specific conditions) reduce to a sheaf cohomology, at least in those situations where their application is justified.
To define 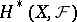 one first constructs the canonical resolution
one first constructs the canonical resolution
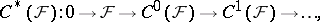 |
where 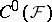 is the sheaf defined by the pre-sheaf
is the sheaf defined by the pre-sheaf 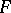 for which
for which 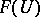 is the group of all (possibly discontinuous) sections of
is the group of all (possibly discontinuous) sections of 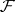 over
over 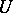 , so that
, so that 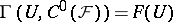 ,
, 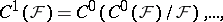
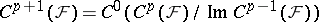 ,
,  . By definition,
. By definition, 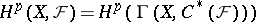 (
(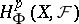 is obtained by replacing the symbol
is obtained by replacing the symbol 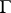 by
by 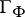 ). The sheaf
). The sheaf 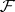 itself can be obtained from
itself can be obtained from 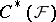 so that
so that 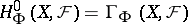 (in classical cohomology
(in classical cohomology 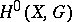 is the group of locally constant functions on
is the group of locally constant functions on 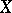 with values in
with values in 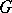 ). The resolution
). The resolution 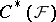 is an exact covariant functor of
is an exact covariant functor of 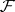 : there is a short exact sequence of resolutions corresponding to a short exact "coefficient" sequence
: there is a short exact sequence of resolutions corresponding to a short exact "coefficient" sequence 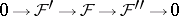 . The functor
. The functor 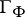 turns out to be exact on the terms
turns out to be exact on the terms 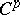 ,
,  , of the resolution, therefore there is an exact cohomology sequence
, of the resolution, therefore there is an exact cohomology sequence
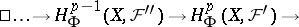 |
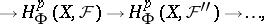 |
corresponding to the indicated coefficient sequence, beginning with 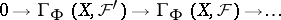 . The cohomology sequence of a pair
. The cohomology sequence of a pair 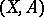 corresponds to the short exact sequence,
corresponds to the short exact sequence, 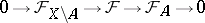 (
(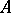 is a closed set).
is a closed set).
The cohomology groups 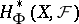 have the following "universality" property, which casts light on their meaning: For any other resolution
have the following "universality" property, which casts light on their meaning: For any other resolution 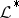 (that is, an exact sequence of sheaves
(that is, an exact sequence of sheaves 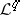 beginning with
beginning with 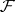 ) there is a natural "comparison" homomorphism
) there is a natural "comparison" homomorphism 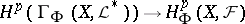 , which is described in terms of
, which is described in terms of 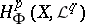 by using spectral sequences. An important case is when the sheaves of the resolution are
by using spectral sequences. An important case is when the sheaves of the resolution are 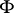 -acyclic, that is, when
-acyclic, that is, when 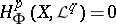 for
for 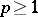 ; in this case the above homomorphism is an isomorphism. The basic examples of acyclic sheaves are flabby sheaves (for all
; in this case the above homomorphism is an isomorphism. The basic examples of acyclic sheaves are flabby sheaves (for all 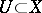 the mappings
the mappings 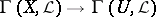 are epimorphic) and soft sheaves (any section over a closed set extends to a section over the whole of
are epimorphic) and soft sheaves (any section over a closed set extends to a section over the whole of 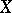 ). The canonical resolution consists of flabby sheaves. If
). The canonical resolution consists of flabby sheaves. If 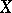 is a paracompact space, then every flabby sheaf is also soft.
is a paracompact space, then every flabby sheaf is also soft.
The universality property enables one to compare cohomologies arising in concrete situations with sheaf cohomology (and consequently also with each other), to discern for them the natural bounds within which their application is effective, and also to apply sheaf-theoretic methods to the solution of concrete problems. For example, Aleksandrov–Čech cohomology (cf. Aleksandrov–Čech homology and cohomology) can be defined using cochains obtained from the cochains of a specially selected system of open coverings by taking the direct limit. These cochains turn out to be sections of the sheaves of germs of cochains (defined analogously to the sheaves of germs of functions) constituting a resolution of the group (or even the sheaf) of coefficients, and this sheaf turns out to be soft if the space is paracompact. Thus, for paracompact spaces Aleksandrov–Čech cohomology coincides with a sheaf cohomology. An analogous conclusion holds for Zariski spaces (in particular, for algebraic varieties). Alexander–Spanier cochains also turn out to be sections of the sheaves of a resolution and, moreover, the resolution consists of soft sheaves if 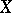 is paracompact, so in this case, in particular, Alexander–Spanier and Aleksandrov–Čech cohomology are naturally isomorphic. In the case of singular cohomology, identification of cochains which coincide on the "small" singular simplices, i.e. subordinated to (arbitrary) open coverings, leads to the so-called localized cochains (giving the same cohomology), which are sections of the sheaves determined by the pre-sheaves of the usual singular cochains. These sheaves turn out to be soft if
is paracompact, so in this case, in particular, Alexander–Spanier and Aleksandrov–Čech cohomology are naturally isomorphic. In the case of singular cohomology, identification of cochains which coincide on the "small" singular simplices, i.e. subordinated to (arbitrary) open coverings, leads to the so-called localized cochains (giving the same cohomology), which are sections of the sheaves determined by the pre-sheaves of the usual singular cochains. These sheaves turn out to be soft if 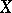 is paracompact (if
is paracompact (if 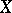 is hereditarily paracompact, then they are also flabby), but they form a resolution only under the additional requirement that
is hereditarily paracompact, then they are also flabby), but they form a resolution only under the additional requirement that 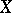 is weakly locally contractible (in every neighbourhood
is weakly locally contractible (in every neighbourhood 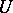 of each point
of each point 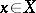 there is a smaller neighbourhood which is contractible to a point inside
there is a smaller neighbourhood which is contractible to a point inside 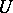 ). A classic example is de Rham's theorem: The cohomology of the complex of differential forms of a differentiable manifold coincides with the usual cohomology with coefficients in the field
). A classic example is de Rham's theorem: The cohomology of the complex of differential forms of a differentiable manifold coincides with the usual cohomology with coefficients in the field 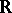 of real numbers (the sheaves of germs of differential forms are soft and form a resolution of
of real numbers (the sheaves of germs of differential forms are soft and form a resolution of 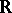 : Sufficiently near to each point each closed differential form is exact).
: Sufficiently near to each point each closed differential form is exact).
There are also resolutions corresponding to any open or locally finite closed covering and these enable one to compare the cohomology of 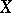 with the cohomology of the coverings (the spectral sequences for coverings). In particular, this gives an isomorphism if
with the cohomology of the coverings (the spectral sequences for coverings). In particular, this gives an isomorphism if 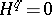 for
for 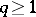 for all elements of the covering and their finite intersections (Leray's theorem). Taking the direct limit with respect to open coverings gives an isomorphism between Aleksandrov–Čech cohomology
for all elements of the covering and their finite intersections (Leray's theorem). Taking the direct limit with respect to open coverings gives an isomorphism between Aleksandrov–Čech cohomology 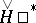 and sheaf cohomology, even for non-paracompact
and sheaf cohomology, even for non-paracompact 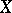 , provided that there are sufficiently many small open sets
, provided that there are sufficiently many small open sets 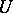 in
in 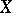 for which
for which 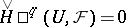 when
when 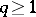 (Cartan's theorem). This means that the cohomologies
(Cartan's theorem). This means that the cohomologies 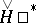 , used in algebraic geometry, with coefficients in coherent sheaves, are also isomorphic to the standard sheaf cohomology
, used in algebraic geometry, with coefficients in coherent sheaves, are also isomorphic to the standard sheaf cohomology 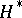 .
.
General constructions ensuring the existence of a comparison homomorphism enable one to compare also the cohomology 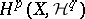 with the hypercohomology
with the hypercohomology 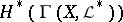 (analogously,
(analogously, 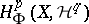 with
with 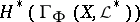 ) in case
) in case 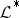 is any differential sheaf (that is, a sheaf in which for any
is any differential sheaf (that is, a sheaf in which for any 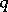 the composition
the composition 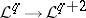 is zero) with
is zero) with 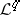 acyclic, where the
acyclic, where the 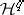 are the derived sheaves of
are the derived sheaves of 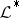 (these are the quotient sheaves of the kernel by the image in each dimension
(these are the quotient sheaves of the kernel by the image in each dimension 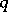 ). The corresponding spectral sequences have many applications. Moreover, if
). The corresponding spectral sequences have many applications. Moreover, if 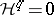 when
when 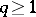 , then
, then 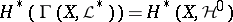 . For example, if in place of
. For example, if in place of 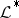 a sheaf of chains
a sheaf of chains 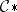 is taken (the boundary operator lowers the dimension by one, the elements of
is taken (the boundary operator lowers the dimension by one, the elements of 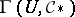 are the chains of the pair
are the chains of the pair 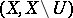 , and the stalk
, and the stalk 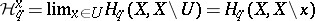 ), then one obtains the way the homology
), then one obtains the way the homology  depends on all the possible
depends on all the possible 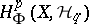 . For a manifold,
. For a manifold, 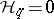 when
when 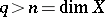 , and
, and 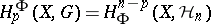 , that is, Poincaré duality holds. If
, that is, Poincaré duality holds. If 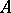 is an open or closed subset of a locally compact space
is an open or closed subset of a locally compact space 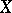 , then the homology of
, then the homology of 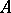 is determined by the sections of
is determined by the sections of 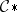 with supports in
with supports in 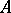 , and the homology of the pair
, and the homology of the pair 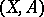 is determined by the sections of the restriction of
is determined by the sections of the restriction of 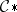 to
to 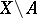 . Conversely (and this is also one of the manifestations of Poincaré duality), if
. Conversely (and this is also one of the manifestations of Poincaré duality), if 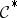 is any flabby resolution for the cohomology, then the restriction of
is any flabby resolution for the cohomology, then the restriction of 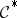 to
to 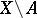 determines the cohomology of
determines the cohomology of 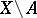 and the sections of
and the sections of 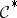 with supports in
with supports in 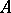 determine the cohomology of the pair
determine the cohomology of the pair 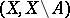 . Since the sheaves
. Since the sheaves  are flabby for manifolds, the homology sequence of the pair
are flabby for manifolds, the homology sequence of the pair 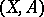 coincides up to an inversion of the numbering with the cohomology sequence of the pair
coincides up to an inversion of the numbering with the cohomology sequence of the pair 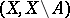 . This means that dualities for manifolds, such as Lefschetz duality
. This means that dualities for manifolds, such as Lefschetz duality 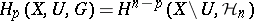 , are particular cases of Poincaré duality. It turns out that the duality relations which are not covered by this scheme are corollaries of Poincaré duality and the acyclicity of the manifold in certain dimensions.
, are particular cases of Poincaré duality. It turns out that the duality relations which are not covered by this scheme are corollaries of Poincaré duality and the acyclicity of the manifold in certain dimensions.
Just such a situation arises in the case of a continuous mapping 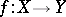 . A resolution for the cohomology of
. A resolution for the cohomology of 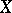 determines a certain differential sheaf
determines a certain differential sheaf 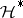 on
on 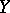 for which the stalks
for which the stalks 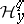 are the direct limits of the cohomology groups
are the direct limits of the cohomology groups 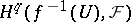 with respect to neighbourhoods
with respect to neighbourhoods 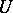 of the points
of the points 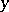 (and for closed mappings
(and for closed mappings 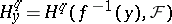 ), where
), where 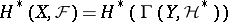 . The way
. The way  depends on
depends on 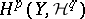 is described by the Leray spectral sequence of the mapping
is described by the Leray spectral sequence of the mapping 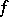 (a particular case of this is the spectral sequence of a Serre fibration). Acyclic mappings correspond to the case when
(a particular case of this is the spectral sequence of a Serre fibration). Acyclic mappings correspond to the case when 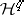 vanishes, thus ensuring that the cohomologies of
vanishes, thus ensuring that the cohomologies of 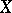 and
and 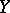 with corresponding coefficients are isomorphic (Vietoris' theorem and its generalizations). The general constructions referred to above also give the spectral sequence of a mapping and take into account (along with their cohomological structure) the degree of disconnectedness of pre-images of points; this is especially effective for zero-dimensional or finite-to-one mappings (in the case of coverings it becomes the Cartan spectral sequence). There are also special spectral sequences in categories of
with corresponding coefficients are isomorphic (Vietoris' theorem and its generalizations). The general constructions referred to above also give the spectral sequence of a mapping and take into account (along with their cohomological structure) the degree of disconnectedness of pre-images of points; this is especially effective for zero-dimensional or finite-to-one mappings (in the case of coverings it becomes the Cartan spectral sequence). There are also special spectral sequences in categories of 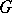 -spaces (spaces on which a group
-spaces (spaces on which a group 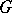 acts).
acts).
In sheaf cohomology there is a natural way of defining a multiplicative structure. The existence of special flabby resolutions, of which the mappings are determined by a certain semi-simplicial structure, enables one to give explicit formulas for the products of cochains, analogous to the usual ones. At the same time this also makes it possible to define other cohomology operations in sheaf theory.
The apparatus of sheaf theory has many applications wherever abstract homological methods are essential: in topology (homological and cohomological dimension, local homology and duality, the structure of various classes of continuous mappings, including imbeddings onto dense subsets, and, in particular, compactifications, etc.), in the theory of analytic manifolds (homology and cohomology with coefficients in coherent analytic sheaves and their applications, cohomology and analytic differential forms, homology and analytic flows (the analogue of de Rham's theorem), etc.), and also in abstract algebraic geometry (the cohomology of affine, projective and complete algebraic varieties with coefficients in coherent algebraic sheaves, algebraic Serre duality, algebraic (combinatorial) dimension, etc.).
Some basic notions of sheaf theory and spectral sequences appeared in the work of J. Leray (1945 and later) in connection with the study of homological properties of continuous mappings of locally compact spaces, and he also gave the definition of cohomology (with compact support) with coefficients in a sheaf. A fairly complete account of sheaf theory using resolutions was later given by H. Cartan. The proof of the de Rham theorem given by A. Weil (1947) and the work of J.-P. Serre (in the early 1950's) on algebraic varieties greatly influenced the development of sheaf theory. Cohomology with coefficients in a sheaf was first defined by the Aleksandrov–Čech method. A mature view of sheaf theory could be found by the end of the 1950's in the work of A. Grothendieck [3] and R. Godement [2], where great generality was achieved and the methods were considerably simplified. E.g., it was shown that the category of sheaves over 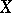 has a generator (that is, a sheaf
has a generator (that is, a sheaf 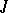 admitting non-zero homomorphisms into any non-zero sheaf; for sheaves of Abelian groups,
admitting non-zero homomorphisms into any non-zero sheaf; for sheaves of Abelian groups, 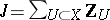 ), and hence that each sheaf can be imbedded in an injective sheaf (Grothendieck's theorem). This is the reason for the formal analogy between cohomology theory with coefficients in sheaves and the theory of derived functors in the module categories: In the category of sheaves over
), and hence that each sheaf can be imbedded in an injective sheaf (Grothendieck's theorem). This is the reason for the formal analogy between cohomology theory with coefficients in sheaves and the theory of derived functors in the module categories: In the category of sheaves over 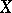 there are "enough" injective objects (although, as a rule, there are few projective objects), and therefore one can freely apply all the corresponding techniques of homological algebra; in particular, one can define the cohomology
there are "enough" injective objects (although, as a rule, there are few projective objects), and therefore one can freely apply all the corresponding techniques of homological algebra; in particular, one can define the cohomology 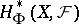 (without any restriction on
(without any restriction on 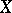 ) as derived functors of the left exact functor
) as derived functors of the left exact functor 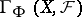 (or even as
(or even as 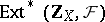 ). This also sheds light, for example, on the general nature of such concepts as the cohomological dimension (over
). This also sheds light, for example, on the general nature of such concepts as the cohomological dimension (over  ) of a space, the algebraic dimension of a variety and the global dimension of a ring. The description given by Grothendieck of the spectral sequence for the functor
) of a space, the algebraic dimension of a variety and the global dimension of a ring. The description given by Grothendieck of the spectral sequence for the functor 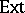 is essential in algebraic geometry. A much simpler method of constructing injective sheaves was found by Godement. He also showed that to construct a cohomology theory it is entirely sufficient to use his canonical flabby resolution, which, from the point of view of homological algebra, turns out to be simply one of the acyclic resolutions of a sheaf. Godement was the first to apply flabby and soft sheaves (soft sheaves are acyclic only for
is essential in algebraic geometry. A much simpler method of constructing injective sheaves was found by Godement. He also showed that to construct a cohomology theory it is entirely sufficient to use his canonical flabby resolution, which, from the point of view of homological algebra, turns out to be simply one of the acyclic resolutions of a sheaf. Godement was the first to apply flabby and soft sheaves (soft sheaves are acyclic only for 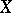 paracompact, which explains their use primarily in topology).
paracompact, which explains their use primarily in topology).
References
| [1] | G.E. Bredon, "Sheaf theory" , McGraw-Hill (1967) |
| [2] | R. Godement, "Topologie algébrique et théorie des faisceaux" , Hermann (1958) |
| [3] | A. Grothendieck, "Sur quelques points d'algèbre homologique" Tohoku Math. J. , 9 (1957) pp. 119–221 |
| [4] | R. Swan, "The theory of sheaves" , Chicago Univ. Press (1964) |
| [5] | E.G. Sklyarenko, "Homology and cohomology of general spaces" , Springer (Forthcoming) (Translated from Russian) |
Comments
Let 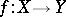 be a continuous mapping between topological spaces and
be a continuous mapping between topological spaces and 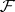 a sheaf on
a sheaf on 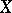 . Then the direct image of
. Then the direct image of 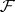 under
under 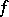 is the sheaf
is the sheaf 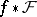 defined by
defined by 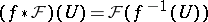 for
for 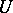 open in
open in 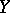 . The functor
. The functor 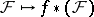 is left-exact on sheaves of modules or Abelian groups. The higher direct images
is left-exact on sheaves of modules or Abelian groups. The higher direct images 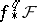 of
of 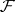 are the right derived functors of
are the right derived functors of 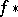 . The sheaf
. The sheaf 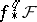 is the sheaf associated to the pre-sheaf
is the sheaf associated to the pre-sheaf 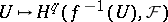 .
.
Given a sheaf 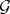 over
over 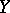 , let
, let 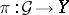 be the associated "sheaf space" (so that
be the associated "sheaf space" (so that 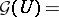 sections of
sections of 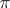 over
over 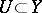 ). Now consider the fibre product (pull-back)
). Now consider the fibre product (pull-back) 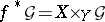 . The inverse image sheaf
. The inverse image sheaf 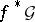 is the sheaf of sections of
is the sheaf of sections of  .
.
The functor  is exact (on sheafs of modules or Abelian groups). The two functors are adjoint to one another:
is exact (on sheafs of modules or Abelian groups). The two functors are adjoint to one another:  .
.
A short sequence of sheaves of Abelian groups or modules 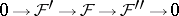 over a space
over a space 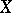 is exact if and only if the corresponding sequence of stalks
is exact if and only if the corresponding sequence of stalks 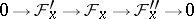 is exact for every
is exact for every 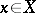 .
.
Grothendieck and his school vastly generalized sheaf theory, from sheaves on a space to the more general notion of sheaves on a site and that of a topos (cf. [a6]–[a8]).
For the theory of coherent sheaves on algebraic varieties see also the fundamental paper [a1]. For the theory of sheaves in the étale topology and for 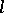 -adic sheaves see [a8], [a12]–[a14].
-adic sheaves see [a8], [a12]–[a14].
For a detailed history of the origins of sheaf theory, see [a1]. The article above focuses almost entirely on the use of sheaf theory in cohomology theory, but it does have many other applications: for example, in the representation theory of rings and other algebraic systems (see, for example, [a3], [a4]), and in logic, in the provision of models for constructive mathematics (see [a2], and also [a9], [a10]).
References
| [a1] | J.W. Gray, "Fragments of the history of sheaf theory" M.P. Fourman (ed.) C.J. Mulvey (ed.) D.S. Scott (ed.) , Applications of sheaves , Lect. notes in math. , 753 , Springer (1979) pp. 1–79 |
| [a2] | M.P. Fourman, D.S. Scott, "Sheaves and logic" M.P. Fourman (ed.) C.J. Mulvey (ed.) D.S. Scott (ed.) , Applications of sheaves , Lect. notes in math. , 753 , Springer (1979) pp. 302–401 |
| [a3] | C.J. Mulvey, "Representations of rings and modules" M.P. Fourman (ed.) C.J. Mulvey (ed.) D.S. Scott (ed.) , Applications of sheaves , Lect. notes in math. , 753 , Springer (1979) pp. 542–585 |
| [a4] | F. Borceux, G. van den Bossche, "Algebra in a localic topos with applications to ring theory" , Lect. notes in math. , 1038 , Springer (1983) |
| [a5] | B.R. Tennison, "Sheaf theory" , Cambridge Univ. Press (1975) |
| [a6] | M. Artin, "Grothendieck topologies" , Harvard Univ. Press (1962) |
| [a7] | P.T. Johnstone, "Topos theory" , Acad. Press (1977) |
| [a8] | A. Grothendieck, et al., "Théorie de topos et cohomologie des schémas (SGA 4–5)" , Lect. notes in math. , 269, 270, 305, 589 , Springer (1972–1977) |
| [a9] | M. Makkai, G.E. Reyes, "First order categorical logic" , Lect. notes in math. , 611 , Springer (1977) |
| [a10] | M. Tierney, "Sheaf theory and the continuum hypothesis" F.W. Lawvere (ed.) , Toposes, algebraic geometry and logic (Dalhousic Univ., Jan. 1971) , Lect. notes in math. , 274 , Springer (1972) pp. 13–42 |
| [a11] | J.-P. Serre, "Faisceaux algébriques cohérents" Ann. of Math. , 61 (1955) pp. 197–278 |
| [a12] | P. Deligne, "Cohomologie étale (SGA 4 1/2)" , Lect. notes in math. , 569 , Springer (1977) |
| [a13] | J.S. Milne, "Etale cohomology" , Princeton Univ. Press (1980) |
| [a14] | E. Freitag, R. Kiehl, "Étale cohomology and the Weil conjecture" , Springer (1988) |
| [a15] | J. Leray, "Sur la forme des espaces topologiques et sur les points fixes des répresentations" J. Math. Pures Appl. , 24 (1945) pp. 95–167 |
| [a16] | J. Leray, "L'anneau spectral et l'anneau fibré d'homologie d'un espace localement compact et d'une application continue" J. Math. Pures Appl. , 29 (1950) pp. 1–139 |
| [a17] | A. Weil, "Foundations of algebraic geometry" , Amer. Math. Soc. (1946) |
| [a18] | , Sem. H. Cartan , 1- , Secr. Math. Inst. H. Poincaré (1948-) |
Sheaf theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sheaf_theory&oldid=14202