Set function
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A mapping 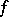 of a certain collection
of a certain collection 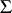 of subsets of a given set
of subsets of a given set 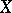 into another set, usually into the real numbers
into another set, usually into the real numbers 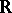 or the complex numbers
or the complex numbers 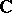 . An important class of set functions are the additive set functions, for which
. An important class of set functions are the additive set functions, for which
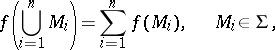 | (*) |
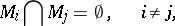 |
and the 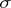 -additive set functions, which satisfy equation (*) for a countably infinite collection of sets also (replace
-additive set functions, which satisfy equation (*) for a countably infinite collection of sets also (replace  by
by 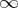 ). If
). If 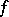 takes only non-negative values,
takes only non-negative values, 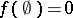 , and
, and 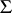 is a
is a 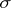 -algebra, then
-algebra, then 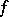 is called a measure.
is called a measure.
References
| [1] | L.V. Kantorovich, G.P. Akilov, "Functional analysis" , Pergamon (1982) (Translated from Russian) |
Comments
References
| [a1] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
How to Cite This Entry:
Set function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Set_function&oldid=15370
Set function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Set_function&oldid=15370
This article was adapted from an original article by V.I. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article