Serre theorem in group cohomology
A theorem proved by J.-P. Serre in 1965 about the cohomology of pro- -groups which has important consequences in group cohomology and representation theory (cf. also Pro-
-groups which has important consequences in group cohomology and representation theory (cf. also Pro- -group; Cohomology of groups). The original proof appeared in [a7], a proof in the context of finite group cohomology appears in [a1].
-group; Cohomology of groups). The original proof appeared in [a7], a proof in the context of finite group cohomology appears in [a1].
Let  denote a fixed prime number and
denote a fixed prime number and  a pro-
a pro- -group, that is, an inverse limit of finite
-group, that is, an inverse limit of finite  -groups (cf. also
-groups (cf. also  -group). Assume that
-group). Assume that  is not an elementary Abelian
is not an elementary Abelian 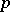 -group (i.e. it is not isomorphic to
-group (i.e. it is not isomorphic to 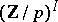 for some indexing set
for some indexing set  , where
, where 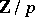 is cyclic of order
is cyclic of order  ). Then Serre's theorem asserts that there exist non-trivial
). Then Serre's theorem asserts that there exist non-trivial 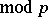 cohomology classes
cohomology classes 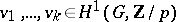 such that the product
such that the product 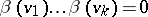 , where
, where 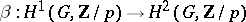 is the Bockstein operation associated to the exact coefficient sequence
is the Bockstein operation associated to the exact coefficient sequence 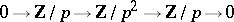 (see [a9] and Cohomology operation). Note that for
(see [a9] and Cohomology operation). Note that for 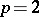 this is simply the squaring operation.
this is simply the squaring operation.
For a finite 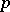 -group, this can be made more explicit as follows. Each cohomology class
-group, this can be made more explicit as follows. Each cohomology class 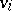 corresponds to a (non-zero) homomorphism
corresponds to a (non-zero) homomorphism 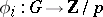 and hence an index-
and hence an index-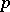 subgroup
subgroup 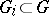 . The class
. The class 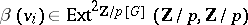 can be represented as an extension class
can be represented as an extension class
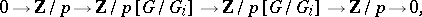 |
where 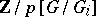 denotes the usual permutation module obtained by induction. When concatenated together, one obtains a representation of the product, which is an element in
denotes the usual permutation module obtained by induction. When concatenated together, one obtains a representation of the product, which is an element in 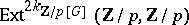 , as
, as
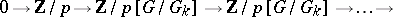 |
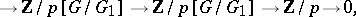 |
which the theorem asserts to be the trivial extension class.
The original application of Serre's result was for proving that if 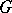 is a profinite group without elements of order
is a profinite group without elements of order  , then the
, then the 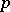 -cohomological dimension of
-cohomological dimension of 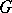 is equal to the
is equal to the 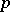 -cohomological dimension of
-cohomological dimension of 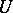 for any open subgroup
for any open subgroup 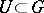 (see [a8] for more on this; cf. also Cohomological dimension).
(see [a8] for more on this; cf. also Cohomological dimension).
However, it is also a basic technical result used in proving the landmark result (see [a5] and [a6]) that the Krull dimension (cf. Dimension) of the 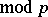 cohomology of a finite group
cohomology of a finite group 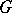 is equal to the rank of the largest elementary Abelian
is equal to the rank of the largest elementary Abelian 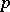 -subgroup in
-subgroup in 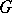 . More precisely, Serre's theorem can be used to verify that for a finite non-Abelian
. More precisely, Serre's theorem can be used to verify that for a finite non-Abelian 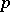 -group
-group  , the Krull dimension of
, the Krull dimension of 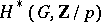 (the maximal rank of a polynomial subalgebra) is determined on maximal proper subgroups, hence leading to an inductive argument which can be reduced to elementary Abelian subgroups.
(the maximal rank of a polynomial subalgebra) is determined on maximal proper subgroups, hence leading to an inductive argument which can be reduced to elementary Abelian subgroups.
This, in turn, can be extended to arbitrary finite groups and to cohomology with coefficients in a modular representation. Indeed, it is a basic result in the theory of complexity and cohomological varieties in representation theory. This is explained [a2], [a3] and [a4].
References
| [a1] | A. Adem, R.J. Milgram, "Cohomology of finite groups" , Grundlehren , 309 , Springer (1994) |
| [a2] | D.J. Benson, "Representations and cohomology II: Cohomology of groups and modules" , Studies in Advanced Math. , 32 , Cambridge Univ. Press (1991) |
| [a3] | J.F. Carlson, "Modules and group algebras" , ETH Lect. Math. , Birkhäuser (1994) |
| [a4] | L. Evens, "Cohomology of groups" , Oxford Univ. Press (1992) |
| [a5] | D. Quillen, "The spectrum of an equivariant cohomology ring I–II" Ann. of Math. , 94 (1971) pp. 549–602 |
| [a6] | D. Quillen, B. Venkov, "Cohomology of finite groups and elementary Abelian subgroups" Topology , 11 (1972) pp. 317–318 |
| [a7] | J.-P. Serre, "Sur la dimension cohomologique des groupes profinis" Topology , 3 (1965) pp. 413–420 |
| [a8] | J.-P. Serre, "Cohomologie Galoisienne" , Lecture Notes in Mathematics , 5 , Springer (1994) (Edition: Fifth) |
| [a9] | E. Spanier, "Algebraic topology" , Springer (1989) |
Serre theorem in group cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Serre_theorem_in_group_cohomology&oldid=12444