Sequential space
A topological space 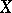 such that if
such that if  and
and  (that is, the set
(that is, the set  is not closed), then there is a sequence
is not closed), then there is a sequence 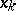 ,
,  of points of
of points of  that converges to a point of
that converges to a point of  . If
. If 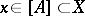 always implies that there is a sequence
always implies that there is a sequence  of points from
of points from 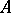 that converges to
that converges to  , then
, then 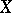 is called a Fréchet–Urysohn space.
is called a Fréchet–Urysohn space.
Comments
Sequential spaces form a coreflective subcategory (see Reflective subcategory) of the category of all topological spaces; the coreflection is obtained by retopologizing an arbitrary space with the topology in which a subset is closed if and only if it is closed under limits of sequences (in the original topology). Spaces which satisfy the first axiom of countability are always sequential (indeed, they are Fréchet–Urysohn spaces), and the sequential spaces form the smallest coreflective subcategory containing all first-countable spaces. For this reason, many topological results which are traditionally proved for first-countable spaces can readily be extended to sequential spaces.
References
| [a1] | R. Engelking, "General topology" , Heldermann (1989) |
Sequential space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sequential_space&oldid=15285