Sequent (in logic)
An expression of the form
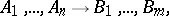 |
where 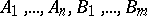 are formulas. It is read as follows. Under the assumptions
are formulas. It is read as follows. Under the assumptions 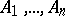 , at least one of
, at least one of 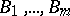 holds. The part of the sequent on the left of the arrow is called the antecedent, and the part on the right the succedent (consequent). The formula
holds. The part of the sequent on the left of the arrow is called the antecedent, and the part on the right the succedent (consequent). The formula 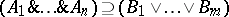 (note that an empty conjunction denotes truth, and an empty disjunction denotes falsity) is called the formula image of the sequent.
(note that an empty conjunction denotes truth, and an empty disjunction denotes falsity) is called the formula image of the sequent.
Comments
Some authors (particularly those working in the context of constructive logic) restrict the term "sequent" to mean an expression of the form
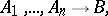 |
i.e. the particular case 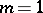 of the above definition.
of the above definition.
For a discussion of Gentzen's sequent calculi cf. Gentzen formal system; Sequent calculus and, e.g., [a2].
References
| [a1] | W. Hodges, "Elementary predicate logic" D. Gabbay (ed.) F. Guenther (ed.) , Handbook of philosophical logic , I , Reidel (1983) pp. 1–131 |
| [a2] | G. Sundholm, "Systems of deduction" D. Gabbay (ed.) F. Guenther (ed.) , Handbook of philosophical logic , I , Reidel (1983) pp. 133–188, §3 |
Sequent (in logic). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sequent_(in_logic)&oldid=17638