Separatrix
A term used in the qualitative theory of differential equations.
1) A separatrix in the original sense of the word is a trajectory 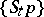 of a flow (continuous-time dynamical system)
of a flow (continuous-time dynamical system) 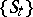 on the plane that tends to a certain equilibrium position
on the plane that tends to a certain equilibrium position 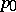 (as
(as 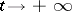 or
or 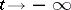 ), and arbitrarily close to it there are trajectories which first approach
), and arbitrarily close to it there are trajectories which first approach 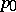 as if they were "going along the trajectory Stp" , and then deviate from it by a certain finite distance. Formally, the latter means the existence of a neighbourhood
as if they were "going along the trajectory Stp" , and then deviate from it by a certain finite distance. Formally, the latter means the existence of a neighbourhood 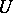 of
of  , a sequence of points
, a sequence of points 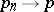 , and sequences of numbers
, and sequences of numbers 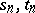 such that as
such that as 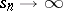 (respectively,
(respectively, 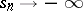 ),
),
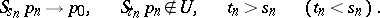 |
The basic example is a separatrix of a non-degenerate (or simple) saddle. For the latter a separatrix can also be understood as a stable (respectively, unstable) manifold, that is, a curve that includes the saddle and both trajectories that tend to it as 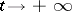 (respectively,
(respectively, 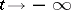 ).
).
The term "separatrix" is connected with the observation that separatrices together with the closed trajectories divide the phase plane into domains in each of which the trajectories behave the same. This observation can be strictly formalized (see [1], [3]). Separatrices can occur in the formation of a limit set of a trajectory. Thus, trajectories can be coiled on a "separatrix loopseparatrix loop" , which is a closed curve formed by a trajectory that tends to one and the same saddle both as 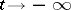 and as
and as 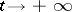 , or on a "separatrix contourseparatrix contour (cycle)" , which is a closed curve consisting of several separatrices that join saddles. Under a small perturbation a separatrix loop can turn into a limit cycle (this is one of the basic types of bifurcation for flows on the plane; see [2], [3]).
, or on a "separatrix contourseparatrix contour (cycle)" , which is a closed curve consisting of several separatrices that join saddles. Under a small perturbation a separatrix loop can turn into a limit cycle (this is one of the basic types of bifurcation for flows on the plane; see [2], [3]).
2) In the multi-dimensional case separatrices (or separatrix manifolds) are most often stable or unstable manifolds of a hyperbolic equilibrium position or periodic trajectory (cf. Hyperbolic point; Hyperbolic set).
Attempts have been made to distinguish by the name "separatrix" a class of trajectories occurring in sets that "separate" in a certain sense trajectories with different behaviour. A direct generalization of the planar case has limited applicability since in the multi-dimensional case the phase space cannot, in general, be partitioned into domains filled by trajectories with the same limit sets (as in the case of a plane, where this situation is "typical" ). The formulations that have been suggested are fairly complicated (see [4]), and one should not expect a complete description of different types of separatrices and of the sets formed from them.
References
| [1] | A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Qualitative theory of second-order dynamic systems" , Wiley (1973) (Translated from Russian) |
| [2] | A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Theory of bifurcations of dynamic systems on a plane" , Israel Program Sci. Transl. (1971) (Translated from Russian) |
| [3] | N.N. Bautin, E.A. Leontovich, "Methods and means for a qualitative investigation of dynamical systems on the plane" , Moscow (1976) (In Russian) |
| [4] | C.S. Hartzman, "Separatrices and singular points" Aequationes Math. , 20 : 1 (1980) pp. 59–72 |
Comments
Cf. also Sector in the theory of ordinary differential equations.
Separatrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Separatrix&oldid=15537