Separable process
A stochastic process such that the behaviour of its trajectories is essentially determined by their behaviour on a countable subset. A real stochastic process  defined on a complete probability space
defined on a complete probability space 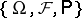 , where
, where 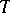 is a subset of the real line
is a subset of the real line  , is separable relative to a class
, is separable relative to a class  of subsets of
of subsets of  if there are a countable set
if there are a countable set 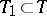 (the separant) and a set
(the separant) and a set 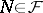 ,
, 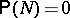 , such that for any
, such that for any 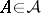 and for any open interval
and for any open interval 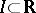 one has
one has
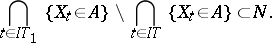 |
Here 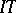 stands for the intersection
stands for the intersection 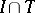 .
.
The concepts of separability relative to the class of closed sets and relative to the class of closed intervals are most important (in the latter case the process is simply called separable). If a process 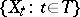 is separable, then for any
is separable, then for any 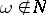 and any open set
and any open set 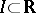 ,
,
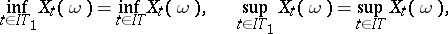 | (1) |
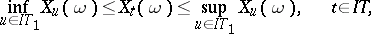 | (2) |
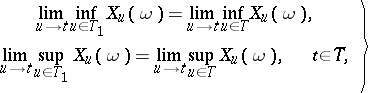 | (3) |
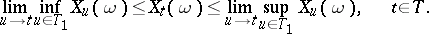 | (4) |
Each of the properties (1)–(4) is equivalent to separability. If 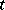 is a left limit point of
is a left limit point of 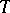 , then there is a sequence
, then there is a sequence 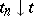 of points of
of points of 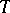 such that
such that
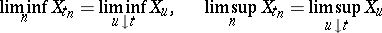 |
with probability 1 (similarly for right limit points). If 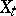 is a separable stochastic process that is continuous in probability, then every countable everywhere-dense set
is a separable stochastic process that is continuous in probability, then every countable everywhere-dense set 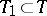 is a separant; in addition, for any open interval
is a separant; in addition, for any open interval 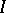 ,
, 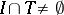 , and any sequence
, and any sequence 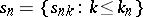 of finite subsets of
of finite subsets of  satisfying the condition
satisfying the condition 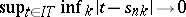 , one has
, one has
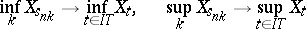 | (5) |
in probability. The convergence in (5) can be replaced by convergence with probability 1 if 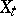 is continuous with probability 1.
is continuous with probability 1.
For any stochastic process 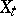 ,
,  , there is a process
, there is a process 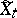 ,
, 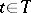 , on the same probability space that is separable relative to the class of closed sets, takes values in the extended real line and is such that
, on the same probability space that is separable relative to the class of closed sets, takes values in the extended real line and is such that  ,
, 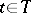 . The concept of separability and its properties can be generalized to processes for which
. The concept of separability and its properties can be generalized to processes for which 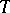 and the range of values are different general topological spaces. The transition to a separable process enables one to assert the measurability of a number of important functionals and sets connected with a process. An alternative approach consists in extending the
and the range of values are different general topological spaces. The transition to a separable process enables one to assert the measurability of a number of important functionals and sets connected with a process. An alternative approach consists in extending the 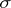 -algebra on which it is defined (for example, in the case of a product of Hausdorff compacta, a measure can be uniquely extended from the usual
-algebra on which it is defined (for example, in the case of a product of Hausdorff compacta, a measure can be uniquely extended from the usual  -algebra generated by cylindrical sets to the very rich
-algebra generated by cylindrical sets to the very rich 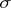 -algebra of Borel sets), rather than in replacing the random variables constituting the process.
-algebra of Borel sets), rather than in replacing the random variables constituting the process.
References
| [1] | J.L. Doob, "Stochastic processes" , Chapman & Hall (1953) |
| [2] | M. Loève, "Probability theory" , Princeton Univ. Press (1963) |
| [3] | I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 1 , Springer (1971) (Translated from Russian) |
| [4] | J.L. Doob, "Probability in function space" Bull. Amer. Math. Soc. , 53 : 1 (1947) pp. 15–30 |
| [5] | E. Nelson, "Regular probability measures on function space" Ann. of Math. , 69 : 3 (1959) pp. 630–643 |
Separable process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Separable_process&oldid=18302