Separable extension
of a field 
An extension 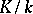 such that for some natural number
such that for some natural number  the fields
the fields  and
and  are linearly disjoint over
are linearly disjoint over 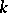 (see Linearly-disjoint extensions). An extension that is not separable is called inseparable. Here
(see Linearly-disjoint extensions). An extension that is not separable is called inseparable. Here 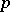 is the characteristic of
is the characteristic of 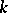 . In characteristic 0 all extensions are separable.
. In characteristic 0 all extensions are separable.
In what follows only algebraic extensions will be considered (for transcendental separable extensions see Transcendental extension). A finite extension is separable if and only if the trace mapping 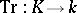 is a non-zero function. An algebraic extension is separable if any finite subextension is separable.
is a non-zero function. An algebraic extension is separable if any finite subextension is separable.
The separable extensions form a distinguished class of extensions, that is, in a tower of fields  the extension
the extension 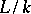 is separable if and only if
is separable if and only if 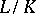 and
and 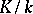 are separable; if
are separable; if  and
and 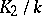 are separable extensions, then so is
are separable extensions, then so is 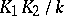 ; for a separable extension
; for a separable extension 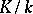 and an arbitrary extension
and an arbitrary extension 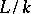 the extension
the extension 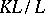 is again separable. An extension
is again separable. An extension 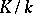 is separable if and only if it admits an imbedding in a Galois extension
is separable if and only if it admits an imbedding in a Galois extension 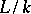 . In this case, the number of different
. In this case, the number of different 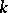 -isomorphisms of
-isomorphisms of 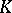 into
into  is the same as the degree
is the same as the degree 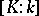 for a finite extension
for a finite extension 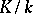 . Any finite separable extension is simple.
. Any finite separable extension is simple.
A polynomial 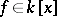 is called separable over
is called separable over  if none of its irreducible factors has a multiple root in an algebraic closure of
if none of its irreducible factors has a multiple root in an algebraic closure of 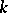 . An algebraic element
. An algebraic element 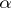 is called separable (over
is called separable (over 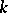 ) if it is a root of a polynomial that is separable over
) if it is a root of a polynomial that is separable over  . Otherwise
. Otherwise  is called inseparable. An element
is called inseparable. An element 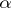 is called purely inseparable over
is called purely inseparable over  if
if  for some
for some  . An irreducible polynomial
. An irreducible polynomial 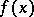 is inseparable if and only if its derivative
is inseparable if and only if its derivative  is identically zero (this is possible only for
is identically zero (this is possible only for 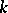 of characteristic
of characteristic  and
and 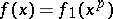 ). An arbitrary irreducible polynomial
). An arbitrary irreducible polynomial 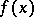 can be uniquely represented in the form
can be uniquely represented in the form 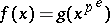 , where
, where  is a separable polynomial. The degree of
is a separable polynomial. The degree of 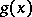 and the number
and the number  are called, respectively, the reduced degree and the index of
are called, respectively, the reduced degree and the index of 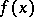 .
.
Let 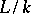 be an arbitrary algebraic extension. The elements of the field
be an arbitrary algebraic extension. The elements of the field 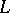 that are separable over
that are separable over 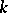 form a field,
form a field, 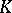 , which is the maximal separable extension of
, which is the maximal separable extension of 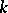 contained in
contained in 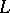 . The field
. The field 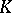 is called the separable closure of
is called the separable closure of 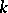 in
in 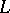 . The degree
. The degree 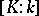 is called the separable degree of
is called the separable degree of 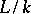 , and the degree
, and the degree 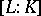 the inseparable degree, or the degree of inseparability. The inseparable degree is equal to some power of the number
the inseparable degree, or the degree of inseparability. The inseparable degree is equal to some power of the number 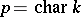 . If
. If 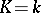 , then
, then 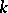 is said to be separably closed in
is said to be separably closed in 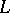 . In this case the extension
. In this case the extension 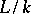 is called purely inseparable. An extension
is called purely inseparable. An extension 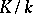 is purely inseparable if and only if
is purely inseparable if and only if
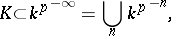 |
that is, if any element of 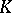 is purely inseparable over
is purely inseparable over 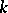 . The purely inseparable extensions of a field
. The purely inseparable extensions of a field 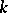 form a distinguished class of extensions. If an extension
form a distinguished class of extensions. If an extension  is both separable and purely inseparable, then
is both separable and purely inseparable, then 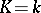 . For references see Extension of a field.
. For references see Extension of a field.
Separable extension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Separable_extension&oldid=17784