Semi-modular lattice
semi-Dedekind lattice
A lattice in which the modularity relation is symmetric, i.e. 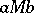 implies
implies 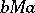 for any lattice elements
for any lattice elements 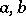 . The modularity relation here is defined as follows: Two elements
. The modularity relation here is defined as follows: Two elements  and
and  are said to constitute a modular pair, in symbols
are said to constitute a modular pair, in symbols 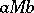 , if
, if 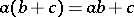 for any
for any 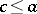 . A lattice in which every pair of elements is modular is called a modular lattice or a Dedekind lattice.
. A lattice in which every pair of elements is modular is called a modular lattice or a Dedekind lattice.
A lattice of finite length is a semi-modular lattice if and only if it satisfies the covering condition: If  and
and 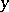 cover
cover 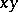 , then
, then 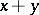 covers
covers  and
and 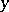 (see Covering element). In any semi-modular lattice of finite length one has the Jordan–Dedekind chain condition (all maximal chains between two fixed elements are of the same length; this makes it possible to develop a theory of dimension in such lattices. A semi-modular lattice of finite length is a relatively complemented lattice if and only if each of its elements is a union of atoms. Such lattices are known as geometric lattices. An important class of semi-modular lattices is that of the "nearly geometric" matroid lattices (see [2]). Every finite lattice is isomorphic to a sublattice of a finite semi-modular lattice. The class of semi-modular lattices is not closed under taking homomorphic images.
(see Covering element). In any semi-modular lattice of finite length one has the Jordan–Dedekind chain condition (all maximal chains between two fixed elements are of the same length; this makes it possible to develop a theory of dimension in such lattices. A semi-modular lattice of finite length is a relatively complemented lattice if and only if each of its elements is a union of atoms. Such lattices are known as geometric lattices. An important class of semi-modular lattices is that of the "nearly geometric" matroid lattices (see [2]). Every finite lattice is isomorphic to a sublattice of a finite semi-modular lattice. The class of semi-modular lattices is not closed under taking homomorphic images.
Besides semi-modular lattices, which are also known as upper semi-modular lattices, one also considers lower semi-modular lattices, which are defined in dual fashion. Examples of semi-modular lattices, apart from modular lattices, are the lattices of all partitions of finite sets and the lattices of linear varieties of affine spaces.
References
| [1] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1967) |
| [2] | F. Maeda, S. Maeda, "Theory of symmetric lattices" , Springer (1970) |
Semi-modular lattice. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-modular_lattice&oldid=16603