Semi-linear mapping
A mapping 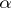 from a (left) module
from a (left) module 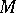 into a (left) module
into a (left) module 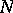 over the same ring
over the same ring 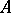 , satisfying the conditions
, satisfying the conditions
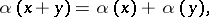 |
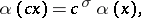 |
where 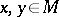 ,
, 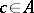 and
and 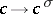 is some automorphism of
is some automorphism of 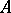 . One says that
. One says that 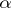 is semi-linear relative to the automorphism
is semi-linear relative to the automorphism 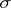 . A semi-linear mapping of vector spaces over the field
. A semi-linear mapping of vector spaces over the field 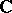 relative to complex conjugation
relative to complex conjugation 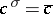 is also known as an anti-linear mapping. A semi-linear mapping of an
is also known as an anti-linear mapping. A semi-linear mapping of an 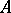 -module
-module 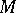 into itself is known as a semi-linear transformation.
into itself is known as a semi-linear transformation.
Example. A homothety of an  -module
-module  , i.e. a mapping
, i.e. a mapping 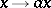 (
( ), where
), where  is a fixed invertible element of
is a fixed invertible element of 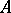 , is a semi-linear mapping relative to the automorphism
, is a semi-linear mapping relative to the automorphism 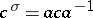 .
.
Many properties of linear mappings and homomorphisms of modules remain valid for semi-linear mappings. In particular, the kernel and image of a semi-linear mapping are submodules; semi-linear mappings of free modules with finite bases are completely determined by their matrices; one can define the rank of a semi-linear mapping of vector spaces, which is equal to the rank of its matrix; etc.
References
| [1] | N. Bourbaki, "Algebra" , Elements of mathematics , 1 , Addison-Wesley (1973) pp. Chapts. I-III (Translated from French) |
Comments
A semi-linear transformation, i.e. a semi-linear mapping of a module into itself, is also called a semi-linear endomorphism.
Semi-linear mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-linear_mapping&oldid=18709