Semi-hyperbolic space

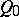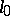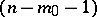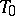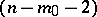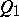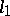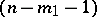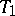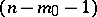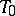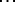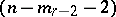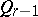A projective -space in which the metric is defined by a given absolute consisting of the following collection: a second-order real cone of index with an -plane vertex ; a real -cone of index with an -plane vertex in the -plane ;; a real -cone of index 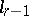with an 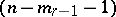-plane vertex 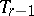; and a non-degenerate real 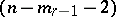-quadric 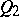of index 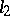in the plane 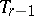; 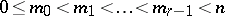. This is the definition of a semi-hyperbolic space with indices 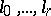; it is denoted by .

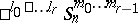If the cone 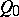is a pair of merging planes, both identical with 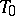(for 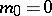), the semi-hyperbolic plane with the improper plane 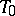is called a semi-Euclidean space:

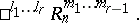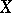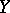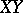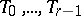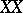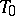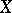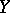The distance between two points and is defined as a function of the position of the straight line relative to the planes . In particular, if does not intersect , the distance between and is defined through a scalar product, in analogy with the appropriate definition in a quasi-hyperbolic space. If 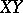intersects 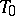but does not intersect 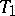, or it intersects 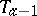but does not intersect 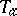, the distance between the points is defined as the scalar product with itself of the distance between the vectors of the points 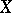and .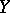

Depending on the position of the absolute relative to the planes 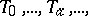one distinguishes four types of straight lines of different orders: elliptic, hyperbolic, isotropic, and parabolic.

The angles between the planes in a semi-hyperbolic space are defined analogous to the angles between the planes in a quasi-hyperbolic space, i.e. using distance in the dual space.

A projective metric in a semi-hyperbolic space is a metric of the most general form. A particular case of such a metric is a metric of a quasi-hyperbolic space. In particular, the -plane 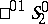is identical with the pseudo-Euclidean space 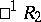, the plane 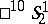— with the co-pseudo-Euclidean space 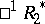; the -spaces 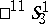and 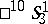coincide with the quasi-hyperbolic -space, the -space 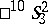— with the co-pseudo-Euclidean space 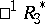, etc. The -space 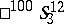is dual to the pseudo-Galilean space 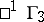, it is known as a co-pseudo-Galilean space; its absolute consists of pairs of real planes (a cone 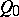) and a point 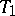on the straight line 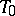in which these planes intersect.

The motions of a semi-hyperbolic space are defined as collineations of the space which map the absolute into itself. If 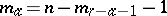and 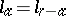, a semi-hyperbolic space is dual to itself. It is then possible to define co-motions, the definition being analogous to that of co-motions in a self-dual quasi-hyperbolic space. The group of motions and the group of motions and co-motions are Lie groups. The motions (and co-motions) of a semi-hyperbolic space are described by pseudo-orthogonal operators with indices determined by the indices of the space.

A semi-hyperbolic space is a semi-Riemannian space.

References

[1]	D.M.Y. Sommerville, Proc. Edinburgh Math. Soc. , 28 (1910) pp. 25–41
[2]	B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian)

References

[a1]	B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian)