|
|
| (One intermediate revision by the same user not shown) |
| Line 1: |
Line 1: |
| − | A family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s0841401.png" /> of operators on a [[Banach space|Banach space]] or [[Topological vector space|topological vector space]] with the property that the composite of any two operators in the family is again a member of the family. If the operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s0841402.png" /> are "indexed" by elements of some abstract [[Semi-group|semi-group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s0841403.png" /> and the binary operation of the latter is compatible with the composition of operators, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s0841404.png" /> is known as a representation of the semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s0841405.png" />. The most detailed attention has been given to one-parameter semi-groups (cf. [[One-parameter semi-group|One-parameter semi-group]]) of bounded linear operators on a Banach space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s0841406.png" />, which yield a representation of the additive semi-group of all positive real numbers, i.e. families <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s0841407.png" /> with the property
| + | <!-- |
| | + | s0841401.png |
| | + | $#A+1 = 469 n = 2 |
| | + | $#C+1 = 469 : ~/encyclopedia/old_files/data/S084/S.0804140 Semi\AAhgroup of operators |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s0841408.png" /></td> </tr></table>
| + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s0841409.png" /> is strongly measurable, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414010.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414011.png" /> is a [[Strongly-continuous semi-group|strongly-continuous semi-group]]; this will be assumed in the sequel. | + | A family $ \{ T \} $ |
| | + | of operators on a [[Banach space|Banach space]] or [[Topological vector space|topological vector space]] with the property that the composite of any two operators in the family is again a member of the family. If the operators $ T $ |
| | + | are "indexed" by elements of some abstract [[Semi-group|semi-group]] $ \mathfrak A $ |
| | + | and the binary operation of the latter is compatible with the composition of operators, $ \{ T \} $ |
| | + | is known as a representation of the semi-group $ \mathfrak A $. |
| | + | The most detailed attention has been given to one-parameter semi-groups (cf. [[One-parameter semi-group|One-parameter semi-group]]) of bounded linear operators on a Banach space $ X $, |
| | + | which yield a representation of the additive semi-group of all positive real numbers, i.e. families $ T ( t) $ |
| | + | with the property |
| | + | |
| | + | $$ |
| | + | T ( t + \tau ) x = T ( t) T ( \tau ) x ,\ t , \tau > 0 ,\ x \in X . |
| | + | $$ |
| | + | |
| | + | If $ T ( t) $ |
| | + | is strongly measurable, $ t > 0 $, |
| | + | then $ T ( t) $ |
| | + | is a [[Strongly-continuous semi-group|strongly-continuous semi-group]]; this will be assumed in the sequel. |
| | | | |
| | The limit | | The limit |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414012.png" /></td> </tr></table>
| + | $$ |
| | + | \omega = \lim\limits _ {t \rightarrow \infty } \ |
| | + | t ^ {-} 1 \mathop{\rm ln} \| T ( t) \| |
| | + | $$ |
| | | | |
| − | exists; it is known as the type of the semi-group. The functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414013.png" /> increase at most exponentially. | + | exists; it is known as the type of the semi-group. The functions $ T ( t) x $ |
| | + | increase at most exponentially. |
| | | | |
| | An important characteristic is the infinitesimal operator (infinitesimal generator) of the semi-group: | | An important characteristic is the infinitesimal operator (infinitesimal generator) of the semi-group: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414014.png" /></td> </tr></table>
| + | $$ |
| | + | A _ {0} x = \lim\limits _ {t \rightarrow 0 } t ^ {-} 1 [ T ( t) x - x ] , |
| | + | $$ |
| | | | |
| − | defined on the linear set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414015.png" /> of all elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414016.png" /> for which the limit exists; the closure, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414017.png" />, of this operator (if it exists) is known as the generating operator, or generator, of the semi-group. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414018.png" /> be the subspace defined as the closure of the union of all values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414019.png" />; then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414020.png" /> is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414021.png" />. If there are no non-zero elements in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414022.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414023.png" />, then the generating operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414024.png" /> exists. In the sequel it will be assumed that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414025.png" /> and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414026.png" /> implies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414027.png" />. | + | defined on the linear set $ D ( A _ {0} ) $ |
| | + | of all elements $ x $ |
| | + | for which the limit exists; the closure, $ A $, |
| | + | of this operator (if it exists) is known as the generating operator, or generator, of the semi-group. Let $ X _ {0} $ |
| | + | be the subspace defined as the closure of the union of all values $ T ( t) x $; |
| | + | then $ D ( A _ {0} ) $ |
| | + | is dense in $ X _ {0} $. |
| | + | If there are no non-zero elements in $ X _ {0} $ |
| | + | such that $ T ( t) x \equiv 0 $, |
| | + | then the generating operator $ A $ |
| | + | exists. In the sequel it will be assumed that $ X _ {0} = X $ |
| | + | and that $ T ( t) x \equiv 0 $ |
| | + | implies $ x = 0 $. |
| | | | |
| − | The simplest class of semi-groups, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414030.png" />, is defined by the condition: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414031.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414032.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414033.png" />. This is equivalent to the condition: The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414034.png" /> is bounded on any interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414035.png" />. In that case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414036.png" /> has a generating operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414037.png" /> whose [[Resolvent|resolvent]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414038.png" /> satisfies the inequalities | + | The simplest class of semi-groups, denoted by $ C _ {0} $, |
| | + | is defined by the condition: $ T ( t) x \rightarrow x $ |
| | + | as $ t \rightarrow 0 $ |
| | + | for any $ x \in X $. |
| | + | This is equivalent to the condition: The function $ \| T ( t) \| $ |
| | + | is bounded on any interval $ ( 0 , a ] $. |
| | + | In that case $ T ( t) $ |
| | + | has a generating operator $ A = A _ {0} $ |
| | + | whose [[Resolvent|resolvent]] $ R ( \lambda , A ) = ( A - \lambda I ) ^ {-} 1 $ |
| | + | satisfies the inequalities |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414039.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table>
| + | $$ \tag{1 } |
| | + | \| R ^ {n} ( \lambda , A ) \| \leq M ( \lambda - \omega ) ^ {-} n ,\ \ |
| | + | n = 1 , 2 , . . . ; \ \lambda > \omega , |
| | + | $$ |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414040.png" /> is the type of the semi-group. Conversely, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414041.png" /> is a [[Closed operator|closed operator]] with domain of definition dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414042.png" /> and with a resolvent satisfying (1), then it is the generating operator of some semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414043.png" /> of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414044.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414045.png" />. Condition (1) is satisfied if | + | where $ \omega $ |
| | + | is the type of the semi-group. Conversely, if $ A $ |
| | + | is a [[Closed operator|closed operator]] with domain of definition dense in $ X $ |
| | + | and with a resolvent satisfying (1), then it is the generating operator of some semi-group $ T ( t) $ |
| | + | of class $ C _ {0} $ |
| | + | such that $ \| T ( t) \| \leq M e ^ {\omega t } $. |
| | + | Condition (1) is satisfied if |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414046.png" /></td> </tr></table>
| + | $$ |
| | + | \| R ( \lambda , A ) \| \leq ( \lambda - \omega ) ^ {-} 1 |
| | + | $$ |
| | | | |
| − | (the Hill–Yosida condition). If, moreover, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414047.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414048.png" /> is a [[Contraction semi-group|contraction semi-group]]: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414049.png" />. | + | (the Hill–Yosida condition). If, moreover, $ \omega = 0 $, |
| | + | then $ T ( t) $ |
| | + | is a [[Contraction semi-group|contraction semi-group]]: $ \| T ( t) \| \leq 1 $. |
| | | | |
| − | A summable semi-group is a semi-group for which the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414050.png" /> are summable on any finite interval for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414051.png" />. A summable semi-group has a generating operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414052.png" />. The operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414053.png" /> is closed if and only if, for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414054.png" />, | + | A summable semi-group is a semi-group for which the functions $ \| T ( t) x \| $ |
| | + | are summable on any finite interval for all $ x \in X $. |
| | + | A summable semi-group has a generating operator $ A = \overline{ {A _ {0} }}\; $. |
| | + | The operator $ A _ {0} $ |
| | + | is closed if and only if, for every $ x \in X $, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414055.png" /></td> </tr></table>
| + | $$ |
| | + | \lim\limits _ {t \rightarrow 0 } |
| | + | \frac{1}{t} |
| | + | \int\limits _ { 0 } ^ { t } T ( s) x d s = x . |
| | + | $$ |
| | | | |
| − | For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414056.png" /> one can define the Laplace transform of a summable semi-group, | + | For $ \mathop{\rm Re} \lambda > \omega $ |
| | + | one can define the Laplace transform of a summable semi-group, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414057.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table>
| + | $$ \tag{2 } |
| | + | \int\limits _ { 0 } ^ \infty e ^ {- \lambda t } T ( t) |
| | + | x d t = - R ( \lambda ) x , |
| | + | $$ |
| | | | |
| − | giving a bounded linear operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414058.png" /> which has many properties of a resolvent operator. | + | giving a bounded linear operator $ R ( \lambda ) $ |
| | + | which has many properties of a resolvent operator. |
| | | | |
| − | A closed operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414059.png" /> with domain of definition dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414060.png" /> is the generating operator of a summable semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414061.png" /> if and only if, for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414062.png" />, the resolvent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414063.png" /> exists for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414064.png" /> and the following conditions hold: a) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414065.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414066.png" />; b) there exist a non-negative function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414067.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414068.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414069.png" />, jointly continuous in all its variables, and a non-negative function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414070.png" />, bounded on any interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414071.png" />, such that, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414072.png" />, | + | A closed operator $ A $ |
| | + | with domain of definition dense in $ X $ |
| | + | is the generating operator of a summable semi-group $ T ( t) $ |
| | + | if and only if, for some $ \omega $, |
| | + | the resolvent $ R ( \lambda , A ) $ |
| | + | exists for $ \mathop{\rm Re} \lambda > \omega $ |
| | + | and the following conditions hold: a) $ \| R ( \lambda , A ) \| \leq M $, |
| | + | $ \mathop{\rm Re} \lambda > \omega $; |
| | + | b) there exist a non-negative function $ \phi ( t , x ) $, |
| | + | $ t > 0 $, |
| | + | $ x \in X $, |
| | + | jointly continuous in all its variables, and a non-negative function $ \phi ( t) $, |
| | + | bounded on any interval $ [ a , b ] \subset ( 0 , \infty ) $, |
| | + | such that, for $ \omega _ {1} > \omega $, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414073.png" /></td> </tr></table>
| + | $$ |
| | + | \int\limits _ { 0 } ^ \infty e ^ {- \omega _ {1} t } \phi ( t , x ) dt < \infty , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414074.png" /></td> </tr></table>
| + | $$ |
| | + | \overline{\lim\limits}\; _ {t \rightarrow \infty } t ^ {-} 1 \mathop{\rm ln} \phi ( t) < \infty |
| | + | ,\ \phi ( t , x ) \leq \phi ( t) \| x \| , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414075.png" /></td> </tr></table>
| + | $$ |
| | + | \| R ^ {n} ( \lambda , A ) x \| \leq |
| | + | \frac{1}{ |
| | + | ( n - 1 ) ! } |
| | + | \int\limits _ { 0 } ^ \infty t ^ {n-} 1 e ^ {- \lambda t } \phi ( t , x ) dt . |
| | + | $$ |
| | | | |
| | Under these conditions | | Under these conditions |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414076.png" /></td> </tr></table>
| + | $$ |
| | + | \| T ( t) x \| \leq \phi ( t , x ) ,\ \ |
| | + | \| T ( t) \| \leq \phi ( t) . |
| | + | $$ |
| | | | |
| − | If one requires in addition that the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414077.png" /> be summable on finite intervals, a necessary and sufficient condition is the existence of a continuous function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414078.png" /> such that, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414079.png" />, | + | If one requires in addition that the function $ \| T ( t) \| $ |
| | + | be summable on finite intervals, a necessary and sufficient condition is the existence of a continuous function $ \phi ( t) $ |
| | + | such that, for $ \omega _ {1} > \omega $, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414080.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table>
| + | $$ \tag{3 } |
| | + | \int\limits _ { 0 } ^ \infty \phi ( t) e ^ {- \omega _ {1} t } dt < \infty , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414081.png" /></td> <td valign="top" style="width:5%;text-align:right;">(4)</td></tr></table>
| + | $$ \tag{4 } |
| | + | \| R ^ {n} ( \lambda , A ) \| \leq |
| | + | \frac{1}{( n - 1 |
| | + | ) ! } |
| | + | \int\limits _ { 0 } ^ \infty t ^ {n-} 1 e ^ {- \lambda t } \phi ( t) dt , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414082.png" /></td> </tr></table>
| + | $$ |
| | + | \lambda > \omega ,\ n= 1 , 2 , . . . . |
| | + | $$ |
| | | | |
| − | Under these conditions, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414083.png" />. By choosing different functions satisfying (3), one can define different subclasses of summable semi-groups. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414084.png" />, the result is the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414085.png" /> and (1) follows from (4). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414086.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414087.png" />, condition (4) implies the condition | + | Under these conditions, $ \| T ( t) \| \leq \phi ( t) $. |
| | + | By choosing different functions satisfying (3), one can define different subclasses of summable semi-groups. If $ \phi ( t) = Me ^ {\omega t } $, |
| | + | the result is the class $ C _ {0} $ |
| | + | and (1) follows from (4). If $ \phi ( t) = Mt ^ {- \alpha } e ^ {\omega t } $, |
| | + | $ 0 \leq \alpha < 1 $, |
| | + | condition (4) implies the condition |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414088.png" /></td> </tr></table>
| + | $$ |
| | + | \| R ^ {n} ( \lambda , A ) \| \leq |
| | + | \frac{M \Gamma ( n - \alpha ) }{( n - 1 ) ! ( \lambda - \omega ) ^ {n - \alpha } } |
| | + | ,\ \ |
| | + | \lambda > \omega ,\ n = 1 , 2 ,\dots. |
| | + | $$ |
| | | | |
| | ==Semi-groups with power singularities.== | | ==Semi-groups with power singularities.== |
| − | If in the previous example <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414089.png" />, then the integrals in (4) are divergent for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414090.png" />. Hence the generating operator for the corresponding semi-group may not have a resolvent for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414091.png" />, i.e. it may have a spectrum equal to the entire complex plane. However, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414092.png" /> large enough one can define for such operators functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414093.png" /> which coincide with the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414094.png" /> in the previous cases. The operator function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414095.png" /> is called a resolvent of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414097.png" /> if it is analytic in some domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414098.png" /> and if for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s08414099.png" />, | + | If in the previous example $ \alpha \geq 1 $, |
| | + | then the integrals in (4) are divergent for $ n \leq \alpha - 1 $. |
| | + | Hence the generating operator for the corresponding semi-group may not have a resolvent for any $ \lambda $, |
| | + | i.e. it may have a spectrum equal to the entire complex plane. However, for $ n $ |
| | + | large enough one can define for such operators functions $ S _ {n} ( \lambda , A ) $ |
| | + | which coincide with the functions $ R ^ {n+} 1 ( \lambda , A ) $ |
| | + | in the previous cases. The operator function $ S _ {n} ( \lambda , A ) $ |
| | + | is called a resolvent of order $ n $ |
| | + | if it is analytic in some domain $ G \subset \mathbf C $ |
| | + | and if for $ \lambda \in G $, |
| | + | |
| | + | $$ |
| | + | S _ {n} ( \lambda , A ) Ax = A S _ {n} ( \lambda , A ) x ,\ \ |
| | + | x \in D ( A) , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140100.png" /></td> </tr></table>
| + | $$ |
| | + | S _ {n} ( \lambda , A ) ( A - \lambda ) ^ {n+} 1 x = x ,\ x \in D ( A ^ {n+} 1 ) , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140101.png" /></td> </tr></table>
| + | and if $ S _ {n} ( \lambda , A ) x = 0 $ |
| | + | for all $ \lambda \in G $ |
| | + | implies $ x = 0 $. |
| | + | If $ \overline{D}\; ( A ^ {n+} 1 ) = X $, |
| | + | the operator may have a unique resolvent of order $ n $, |
| | + | for which there is a maximal domain of analyticity, known as the resolvent set of order $ n $. |
| | | | |
| − | and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140102.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140103.png" /> implies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140104.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140105.png" />, the operator may have a unique resolvent of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140106.png" />, for which there is a maximal domain of analyticity, known as the resolvent set of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140108.png" />.
| + | Let $ T ( t) $ |
| | + | be a strongly-continuous semi-group such that the inequality |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140109.png" /> be a strongly-continuous semi-group such that the inequality
| + | $$ |
| | + | \| T ( t) \| \leq M t ^ {- \alpha } e ^ {\omega t } |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140110.png" /></td> </tr></table>
| + | holds for $ \alpha \geq 1 $. |
| | + | Then its generating operator $ B $ |
| | + | has a resolvent of order $ n $ |
| | + | for $ n > \alpha - 1 $, |
| | + | and, moreover, |
| | | | |
| − | holds for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140111.png" />. Then its generating operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140112.png" /> has a resolvent of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140113.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140114.png" />, and, moreover,
| + | $$ |
| | + | S _ {n} ( \lambda , B ) x = \ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140115.png" /></td> </tr></table>
| + | \frac{1}{n!} |
| | + | \int\limits _ { 0 } ^ \infty t ^ {n} e ^ {- \lambda t } T |
| | + | ( t) x dt ,\ \mathop{\rm Re} \lambda > \omega , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140116.png" /></td> <td valign="top" style="width:5%;text-align:right;">(5)</td></tr></table>
| + | $$ \tag{5 } |
| | + | \left \| |
| | + | \frac{d ^ {k} S _ {n} ( \lambda , B ) }{d \lambda ^ {k} } |
| | + | x \right \| \leq |
| | + | \frac{M \Gamma ( k + n + 1 - \alpha ) }{n |
| | + | ! ( \mathop{\rm Re} \lambda - \omega ) ^ {k + n + 1 - \alpha } } |
| | + | , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140117.png" /></td> </tr></table>
| + | $$ |
| | + | \mathop{\rm Re} \lambda > \omega ,\ k = 0 , 1 ,\dots . |
| | + | $$ |
| | | | |
| − | Conversely, suppose that for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140118.png" /> the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140119.png" /> has a resolvent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140120.png" /> of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140121.png" /> satisfying (5) with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140122.png" />. Then there exists a unique semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140123.png" /> such that | + | Conversely, suppose that for $ \mathop{\rm Re} \lambda > 0 $ |
| | + | the operator $ B $ |
| | + | has a resolvent $ S _ {n} ( \lambda , B ) $ |
| | + | of order $ n $ |
| | + | satisfying (5) with $ n > \alpha - 1 $. |
| | + | Then there exists a unique semi-group $ T ( t) $ |
| | + | such that |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140124.png" /></td> </tr></table>
| + | $$ |
| | + | \| T ( t) \| \leq M t ^ {- \alpha } e ^ {\omega t } , |
| | + | $$ |
| | | | |
| − | and the generating operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140125.png" /> of this semi-group is such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140126.png" />. | + | and the generating operator $ A $ |
| | + | of this semi-group is such that $ S _ {n} ( \lambda , A ) = S _ {n} ( \lambda , B ) $. |
| | | | |
| | ==Smooth semi-groups.== | | ==Smooth semi-groups.== |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140127.png" />, the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140128.png" /> is continuously differentiable and | + | If $ x \in D ( A _ {0} ) $, |
| | + | the function $ T ( t) x $ |
| | + | is continuously differentiable and |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140129.png" /></td> </tr></table>
| + | $$ |
| | | | |
| − | There exist semi-groups of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140130.png" /> such that, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140131.png" />, the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140132.png" /> are non-differentiable for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140133.png" />. However, there are important classes of semi-groups for which the degree of smoothness increases with increasing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140134.png" />. If the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140135.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140136.png" />, are differentiable for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140137.png" />, then it follows from the semi-group property that the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140138.png" /> are twice differentiable if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140139.png" />, three times differentiable if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140140.png" />, etc. Therefore, if these functions are differentiable at any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140141.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140142.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140143.png" /> is infinitely differentiable.
| + | \frac{d T ( t) }{dt} |
| | + | x = A _ {0} T |
| | + | ( t) x = T ( t) A _ {0} x . |
| | + | $$ |
| | | | |
| − | Given a semi-group of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140144.png" />, a necessary and sufficient condition for the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140145.png" /> to be differentiable for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140146.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140147.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140148.png" />, is that there exist numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140149.png" /> such that the resolvent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140150.png" /> is defined in the domain
| + | There exist semi-groups of class $ C _ {0} $ |
| | + | such that, if $ x \notin D ( A _ {0} ) = D ( A) $, |
| | + | the functions $ T ( t) x $ |
| | + | are non-differentiable for all $ t $. |
| | + | However, there are important classes of semi-groups for which the degree of smoothness increases with increasing $ t $. |
| | + | If the functions $ T ( t) x $, |
| | + | $ t > t _ {0} $, |
| | + | are differentiable for any $ x \in X $, |
| | + | then it follows from the semi-group property that the $ T ( t) x $ |
| | + | are twice differentiable if $ t > 2 t _ {0} $, |
| | + | three times differentiable if $ t > 3 t _ {0} $, |
| | + | etc. Therefore, if these functions are differentiable at any $ t > 0 $ |
| | + | for $ x \in X $, |
| | + | then $ T ( t) x $ |
| | + | is infinitely differentiable. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140151.png" /></td> </tr></table>
| + | Given a semi-group of class $ C _ {0} $, |
| | + | a necessary and sufficient condition for the functions $ T ( t) x $ |
| | + | to be differentiable for all $ x \in X $ |
| | + | and $ t > t _ {0} $, |
| | + | where $ t _ {0} \geq 0 $, |
| | + | is that there exist numbers $ a , b , c > 0 $ |
| | + | such that the resolvent $ R ( \lambda , A ) $ |
| | + | is defined in the domain |
| | + | |
| | + | $$ |
| | + | \mathop{\rm Re} \lambda > a - b \mathop{\rm ln} | \mathop{\rm Im} \lambda | , |
| | + | $$ |
| | | | |
| | while in this domain | | while in this domain |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140152.png" /></td> </tr></table>
| + | $$ |
| | + | \| R( \lambda , A ) \| \leq c | \mathop{\rm Im} \lambda | . |
| | + | $$ |
| | | | |
| − | A necessary and sufficient condition for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140153.png" /> to be infinitely differentiable for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140154.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140155.png" /> is that, for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140156.png" />, there exist <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140157.png" /> such that the resolvent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140158.png" /> is defined in the domain | + | A necessary and sufficient condition for $ T ( t) x $ |
| | + | to be infinitely differentiable for all $ x \in X $ |
| | + | and $ t > 0 $ |
| | + | is that, for every $ b > 0 $, |
| | + | there exist $ a _ {b} , c _ {b} $ |
| | + | such that the resolvent $ R ( \lambda , A ) $ |
| | + | is defined in the domain |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140159.png" /></td> </tr></table>
| + | $$ |
| | + | \mathop{\rm Re} \lambda > a _ {b} - b \mathop{\rm ln} | \mathop{\rm Im} \lambda | , |
| | + | $$ |
| | | | |
| | and such that | | and such that |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140160.png" /></td> </tr></table>
| + | $$ |
| | + | \| R ( \lambda , A ) \| \leq c _ {b} | \mathop{\rm Im} \lambda | . |
| | + | $$ |
| | | | |
| − | Sufficient conditions are: If there exists a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140161.png" /> for which | + | Sufficient conditions are: If there exists a $ \mu > \omega $ |
| | + | for which |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140162.png" /></td> </tr></table>
| + | $$ |
| | + | \overline{\lim\limits}\; _ {\tau \rightarrow \infty } \mathop{\rm ln} | \tau | \| R ( \mu + i \tau , A ) \| = t _ {0} < \infty , |
| | + | $$ |
| | | | |
| − | then the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140163.png" /> are differentiable for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140164.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140165.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140166.png" />, then the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140167.png" /> are infinitely differentiable for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140168.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140169.png" />. | + | then the $ T ( t) x $ |
| | + | are differentiable for $ t > t _ {0} $ |
| | + | and $ x \in X $; |
| | + | if $ t _ {0} = 0 $, |
| | + | then the $ T ( t) x $ |
| | + | are infinitely differentiable for all $ t > 0 $ |
| | + | and $ x \in X $. |
| | | | |
| − | The degree of smoothness of a semi-group may sometimes be inferred from its behaviour at zero; for example, suppose that for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140170.png" /> there exists a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140171.png" /> such that, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140172.png" />, | + | The degree of smoothness of a semi-group may sometimes be inferred from its behaviour at zero; for example, suppose that for every $ c > 0 $ |
| | + | there exists a $ \delta _ {c} $ |
| | + | such that, for $ 0 < t < \delta _ {c} $, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140173.png" /></td> </tr></table>
| + | $$ |
| | + | \| I - T ( t) \| \leq 2 - ct \mathop{\rm ln} t ^ {-} 1 , |
| | + | $$ |
| | | | |
| − | then the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140174.png" /> are infinitely differentiable for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140175.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140176.png" />. | + | then the $ T ( t) x $ |
| | + | are infinitely differentiable for all $ t > 0 $, |
| | + | $ x \in X $. |
| | | | |
| − | There are smoothness conditions for summable semi-groups and semi-groups of polynomial growth. If a semi-group has polynomial growth of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140177.png" /> and is infinitely differentiable for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140178.png" />, then the function | + | There are smoothness conditions for summable semi-groups and semi-groups of polynomial growth. If a semi-group has polynomial growth of degree $ \alpha $ |
| | + | and is infinitely differentiable for $ t > 0 $, |
| | + | then the function |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140179.png" /></td> </tr></table>
| + | $$ |
| | + | |
| | + | \frac{d T ( t) }{dt} |
| | + | x = A T ( t) x |
| | + | $$ |
| | | | |
| | also has polynomial growth: | | also has polynomial growth: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140180.png" /></td> </tr></table>
| + | $$ |
| | + | \| A T ( t) \| \leq M _ {1} t ^ {- \beta } e ^ {\omega t } . |
| | + | $$ |
| | | | |
| − | In the general case there is no rigorous relationship between the numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140181.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140182.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140183.png" /> can be utilized for a more detailed classification of infinitely-differentiable semi-groups of polynomial growth. | + | In the general case there is no rigorous relationship between the numbers $ \alpha $ |
| | + | and $ \beta $, |
| | + | and $ \beta $ |
| | + | can be utilized for a more detailed classification of infinitely-differentiable semi-groups of polynomial growth. |
| | | | |
| | ==Analytic semi-groups.== | | ==Analytic semi-groups.== |
| − | An important class of semi-groups, related to partial differential equations of parabolic type, comprises those semi-groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140184.png" /> which admit an analytic continuation to some sector of the complex plane containing the positive real axis. A semi-group of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140185.png" /> has this property if and only if its resolvent satisfies the following inequality in some right half-plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140186.png" />: | + | An important class of semi-groups, related to partial differential equations of parabolic type, comprises those semi-groups $ T ( t) $ |
| | + | which admit an analytic continuation to some sector of the complex plane containing the positive real axis. A semi-group of class $ C _ {0} $ |
| | + | has this property if and only if its resolvent satisfies the following inequality in some right half-plane $ \mathop{\rm Re} \lambda > \omega $: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140187.png" /></td> </tr></table>
| + | $$ |
| | + | \| R ( \lambda , A ) \| \leq M | \lambda - \omega | ^ {-} 1 . |
| | + | $$ |
| | | | |
| | Another necessary and sufficient conditions is: The semi-group is strongly differentiable and its derivative satisfies the estimate | | Another necessary and sufficient conditions is: The semi-group is strongly differentiable and its derivative satisfies the estimate |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140188.png" /></td> </tr></table>
| + | $$ |
| | + | \left \| |
| | + | \frac{d T }{dt} |
| | + | ( t) \right \| \leq M t ^ {-} 1 e ^ {\omega t } . |
| | + | $$ |
| | | | |
| | Finally, the inequality | | Finally, the inequality |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140189.png" /></td> </tr></table>
| + | $$ |
| | + | \overline{\lim\limits}\; _ {t \rightarrow 0 } \| I - T ( t) \| < 2 |
| | + | $$ |
| | | | |
| − | is also a sufficient condition for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140190.png" /> to be analytic. | + | is also a sufficient condition for $ T ( t) $ |
| | + | to be analytic. |
| | | | |
| − | If a semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140191.png" /> has an analytic continuation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140192.png" /> to a sector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140193.png" /> and has polynomial growth at zero, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140194.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140195.png" />, then the resolvent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140196.png" /> of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140197.png" /> of its generating operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140198.png" /> has an analytic continuation to the sector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140199.png" />, and satisfies the following estimate in any sector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140200.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140201.png" />: | + | If a semi-group $ T ( t) $ |
| | + | has an analytic continuation $ T ( z) $ |
| | + | to a sector $ | \mathop{\rm arg} z | < \phi \leq \pi / 2 $ |
| | + | and has polynomial growth at zero, $ \| T ( z) \| \leq c | z | ^ \alpha $, |
| | + | $ \alpha > 0 $, |
| | + | then the resolvent $ S _ {n} ( \lambda , A ) $ |
| | + | of order $ n > \alpha - 1 $ |
| | + | of its generating operator $ A $ |
| | + | has an analytic continuation to the sector $ | \mathop{\rm arg} \lambda | \leq \pi / 2 + \phi $, |
| | + | and satisfies the following estimate in any sector $ | \mathop{\rm arg} \lambda | \leq \pi / 2 + \psi $, |
| | + | $ \psi < \phi $: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140202.png" /></td> </tr></table>
| + | $$ |
| | + | \| S _ {n} ( \lambda , A ) \| \leq | \lambda | ^ |
| | + | {\alpha - n - 1 } M ( \psi ) . |
| | + | $$ |
| | | | |
| − | Conversely, suppose that the resolvent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140203.png" /> of an operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140204.png" /> is defined in a sector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140205.png" /> and that | + | Conversely, suppose that the resolvent $ S _ {n} ( \lambda , B ) $ |
| | + | of an operator $ B $ |
| | + | is defined in a sector $ | \mathop{\rm arg} \lambda | \leq \pi / 2 + \psi $ |
| | + | and that |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140206.png" /></td> </tr></table>
| + | $$ |
| | + | \| S _ {n} ( \lambda , B ) \| \leq \lambda ^ {\alpha - n - 1 } M . |
| | + | $$ |
| | | | |
| − | Then there exists a semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140207.png" /> of growth <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140208.png" />, analytic in the sector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140209.png" />, whose generating operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140210.png" /> is such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140211.png" />. | + | Then there exists a semi-group $ T ( z) $ |
| | + | of growth $ \alpha $, |
| | + | analytic in the sector $ | \mathop{\rm arg} z | < \psi $, |
| | + | whose generating operator $ A $ |
| | + | is such that $ S _ {n} ( \lambda , A ) = S _ {n} ( \lambda , B ) $. |
| | | | |
| | ==Distribution semi-groups.== | | ==Distribution semi-groups.== |
| − | In accordance with the general concept of the theory of distributions (cf. [[Generalized function|Generalized function]]), one can drop the requirement that the operator-valued function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140212.png" /> be defined for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140213.png" />, demanding only that it be possible to evaluate the integrals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140214.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140215.png" /> in the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140216.png" /> of infinitely-differentiable functions with compact support. Hence the following definition: A distribution semi-group on a Banach space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140217.png" /> is a continuous linear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140218.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140219.png" /> into the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140220.png" /> of all bounded linear operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140221.png" />, with the following properties: a) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140222.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140223.png" />; b) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140224.png" /> are functions in the subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140225.png" /> of all functions in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140226.png" /> with support in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140227.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140228.png" />, where the star denotes convolution: | + | In accordance with the general concept of the theory of distributions (cf. [[Generalized function|Generalized function]]), one can drop the requirement that the operator-valued function $ T ( t) $ |
| | + | be defined for every $ t > 0 $, |
| | + | demanding only that it be possible to evaluate the integrals $ \int _ {- \infty } ^ {+ \infty } T ( t) \phi ( t) dt $ |
| | + | for all $ \phi $ |
| | + | in the space $ D ( \mathbf R ) $ |
| | + | of infinitely-differentiable functions with compact support. Hence the following definition: A distribution semi-group on a Banach space $ X $ |
| | + | is a continuous linear mapping $ T ( \phi ) $ |
| | + | of $ D ( \mathbf R ) $ |
| | + | into the space $ L ( X) $ |
| | + | of all bounded linear operators on $ X $, |
| | + | with the following properties: a) $ T ( \phi ) = 0 $ |
| | + | if $ \supp \phi \subset ( - \infty , 0 ) $; |
| | + | b) if $ \phi , \psi $ |
| | + | are functions in the subspace $ D ^ {+} ( \mathbf R ) $ |
| | + | of all functions in $ D ( \mathbf R ) $ |
| | + | with support in $ ( 0 , \infty ) $, |
| | + | then $ T ( \phi * \psi ) = T ( \phi ) T ( \psi ) $, |
| | + | where the star denotes convolution: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140229.png" /></td> </tr></table>
| + | $$ |
| | + | \phi * \psi = \int\limits _ {- \infty } ^ \infty \phi ( t - s ) \psi ( s) d s |
| | + | $$ |
| | | | |
| − | (the semi-group property); c) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140230.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140231.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140232.png" />; d) the linear hull of the set of all values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140233.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140234.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140235.png" />, is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140236.png" />; e) for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140237.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140238.png" />, there exists a continuous <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140239.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140240.png" /> with values in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140241.png" />, so that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140242.png" /> and | + | (the semi-group property); c) if $ T ( \phi ) x = 0 $ |
| | + | for all $ \phi \in D ^ {+} ( \mathbf R ) $, |
| | + | then $ x = 0 $; |
| | + | d) the linear hull of the set of all values of $ T ( \phi ) x $, |
| | + | $ \phi \in D ^ {+} ( \mathbf R ) $, |
| | + | $ x \in X $, |
| | + | is dense in $ X $; |
| | + | e) for any $ y = T ( \psi ) x $, |
| | + | $ \psi \in D ^ {+} ( \mathbf R ) $, |
| | + | there exists a continuous $ u ( t) $ |
| | + | on $ ( 0 , \infty ) $ |
| | + | with values in $ X $, |
| | + | so that $ u( 0) = y $ |
| | + | and |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140243.png" /></td> </tr></table>
| + | $$ |
| | + | T ( \phi ) y = \int\limits _ { 0 } ^ \infty \phi ( t) u ( t) dt |
| | + | $$ |
| | | | |
| − | for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140244.png" />. | + | for all $ \phi \in D ( \mathbf R ) $. |
| | | | |
| − | The infinitesimal operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140245.png" /> of a distribution semi-group is defined as follows. If there exists a delta-sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140246.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140247.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140248.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140249.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140250.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140251.png" />. The infinitesimal operator has a closure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140252.png" />, known as the infinitesimal generator of the distribution semi-group. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140253.png" /> is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140254.png" /> and contains <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140255.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140256.png" />. | + | The infinitesimal operator $ A _ {0} $ |
| | + | of a distribution semi-group is defined as follows. If there exists a delta-sequence $ \{ \rho _ {n} \} \subset D ^ {+} ( \mathbf R ) $ |
| | + | such that $ T ( \rho _ {n} ) x \rightarrow x $ |
| | + | and $ T ( - \rho _ {n} ^ \prime ) x \rightarrow y $ |
| | + | as $ n \rightarrow \infty $, |
| | + | then $ x \in D ( A _ {0} ) $ |
| | + | and $ y = A _ {0} x $. |
| | + | The infinitesimal operator has a closure $ A = \overline{ {A _ {0} }}\; $, |
| | + | known as the infinitesimal generator of the distribution semi-group. The set $ \cap _ {n=} 1 ^ \infty D ( A _ {0} ^ {n} ) $ |
| | + | is dense in $ X $ |
| | + | and contains $ T ( \phi ) X $ |
| | + | for any $ \phi \in D ^ {+} ( \mathbf R ) $. |
| | | | |
| − | A closed linear operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140257.png" /> with a dense domain of definition in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140258.png" /> is the infinitesimal generator of a distribution semi-group if and only if there exist numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140259.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140260.png" /> and a natural number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140261.png" /> such that the resolvent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140262.png" /> exists for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140263.png" /> and satisfies the inequality | + | A closed linear operator $ A $ |
| | + | with a dense domain of definition in $ X $ |
| | + | is the infinitesimal generator of a distribution semi-group if and only if there exist numbers $ a , b \geq 0 $, |
| | + | $ c > 0 $ |
| | + | and a natural number $ m $ |
| | + | such that the resolvent $ R ( \lambda , A ) $ |
| | + | exists for $ \mathop{\rm Re} \lambda \geq a \mathop{\rm ln} ( 1 + | \lambda | ) + b $ |
| | + | and satisfies the inequality |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140264.png" /></td> <td valign="top" style="width:5%;text-align:right;">(6)</td></tr></table>
| + | $$ \tag{6 } |
| | + | \| R ( \lambda , A ) \| \leq c ( 1 + | \lambda | ) ^ {m} . |
| | + | $$ |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140265.png" /> is a closed linear operator on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140266.png" />, then the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140267.png" /> can be made into a [[Fréchet space|Fréchet space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140268.png" /> by introducing the system of norms | + | If $ A $ |
| | + | is a closed linear operator on $ X $, |
| | + | then the set $ \cap _ {n=} 1 ^ \infty D ( A ^ {n} ) $ |
| | + | can be made into a [[Fréchet space|Fréchet space]] $ X _ \infty $ |
| | + | by introducing the system of norms |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140269.png" /></td> </tr></table>
| + | $$ |
| | + | \| x \| _ {n} = \ |
| | + | \sum _ { k= } 0 ^ { n } \| A ^ {k} x \| . |
| | + | $$ |
| | | | |
| − | The restriction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140270.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140271.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140272.png" /> leaves <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140273.png" /> invariant. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140274.png" /> is the infinitesimal generator of a semi-group, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140275.png" /> is the infinitesimal generator of a semi-group of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140276.png" /> (continuous for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140277.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140278.png" />) on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140279.png" />. Conversely, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140280.png" /> is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140281.png" />, the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140282.png" /> has a non-empty resolvent set and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140283.png" /> is the infinitesimal generator of a semi-group of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140284.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140285.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140286.png" /> is the infinitesimal generator of a distribution semi-group on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140287.png" />. | + | The restriction $ A _ \infty $ |
| | + | of $ A $ |
| | + | to $ X _ \infty $ |
| | + | leaves $ X _ \infty $ |
| | + | invariant. If $ A $ |
| | + | is the infinitesimal generator of a semi-group, then $ A _ \infty $ |
| | + | is the infinitesimal generator of a semi-group of class $ C _ {0} $( |
| | + | continuous for $ t \geq 0 $, |
| | + | $ T ( 0 ) = I $) |
| | + | on $ X _ \infty $. |
| | + | Conversely, if $ X _ \infty $ |
| | + | is dense in $ X $, |
| | + | the operator $ A $ |
| | + | has a non-empty resolvent set and $ A $ |
| | + | is the infinitesimal generator of a semi-group of class $ C _ {0} $ |
| | + | on $ X _ \infty $, |
| | + | then $ A $ |
| | + | is the infinitesimal generator of a distribution semi-group on $ X $. |
| | | | |
| − | A distribution semi-group has exponential growth of order at most <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140288.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140289.png" />, if there exists an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140290.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140291.png" /> is a continuous mapping in the topology induced on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140292.png" /> by the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140293.png" /> of rapidly-decreasing functions. A closed linear operator is the infinitesimal generator of a distribution semi-group with the above property if and only if it has a resolvent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140294.png" /> which satisfies (6) in the domain | + | A distribution semi-group has exponential growth of order at most $ q $, |
| | + | $ 1 \leq q < \infty $, |
| | + | if there exists an $ \omega > 0 $ |
| | + | such that $ \mathop{\rm exp} ( - \omega t ^ {q} ) T ( \phi ) $ |
| | + | is a continuous mapping in the topology induced on $ D ^ {+} $ |
| | + | by the space $ S ( \mathbf R ) $ |
| | + | of rapidly-decreasing functions. A closed linear operator is the infinitesimal generator of a distribution semi-group with the above property if and only if it has a resolvent $ R ( \lambda , A ) $ |
| | + | which satisfies (6) in the domain |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140295.png" /></td> </tr></table>
| + | $$ |
| | + | \{ \lambda : { \mathop{\rm Re} \lambda \geq [ \alpha \mathop{\rm ln} ( 1 + | \mathop{\rm Im} \ |
| | + | \lambda | + \beta ) ] ^ {1- 1/q } , \mathop{\rm Re} \lambda > \omega } \} |
| | + | , |
| | + | $$ |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140296.png" />. In particular, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140297.png" /> the semi-group is said to be exponential and inequality (6) is valid in some half-plane. There exists a characterization of the semi-groups of the above types in terms of the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140298.png" />. Questions of smoothness and analyticity have also been investigated for distribution semi-groups. | + | where $ \alpha , \beta > 0 $. |
| | + | In particular, if $ q = 1 $ |
| | + | the semi-group is said to be exponential and inequality (6) is valid in some half-plane. There exists a characterization of the semi-groups of the above types in terms of the operator $ A _ \infty $. |
| | + | Questions of smoothness and analyticity have also been investigated for distribution semi-groups. |
| | | | |
| − | ==Semi-groups of operators in a (separable) locally convex space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140299.png" />.== | + | ==Semi-groups of operators in a (separable) locally convex space $ X $.== |
| − | The definition of a strongly-continuous semi-group of operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140300.png" /> continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140301.png" /> remains the same as for a Banach space. Similarly, the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140302.png" /> is defined by the property <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140303.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140304.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140305.png" />. A semi-group is said to be locally equicontinuous (of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140308.png" />) if the family of operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140309.png" /> is equicontinuous when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140310.png" /> ranges over any finite interval in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140311.png" />. In a [[Barrelled space|barrelled space]], a semi-group of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140312.png" /> is always equicontinuous (cf. [[Equicontinuity|Equicontinuity]]). | + | The definition of a strongly-continuous semi-group of operators $ T ( t ) $ |
| | + | continuous on $ X $ |
| | + | remains the same as for a Banach space. Similarly, the class $ C _ {0} $ |
| | + | is defined by the property $ T ( t ) x \rightarrow x $ |
| | + | as $ t \rightarrow 0 $ |
| | + | for any $ x \in X $. |
| | + | A semi-group is said to be locally equicontinuous (of class $ lC _ {0} $) |
| | + | if the family of operators $ T ( t ) $ |
| | + | is equicontinuous when $ t $ |
| | + | ranges over any finite interval in $ ( 0 , \infty ) $. |
| | + | In a [[Barrelled space|barrelled space]], a semi-group of class $ C _ {0} $ |
| | + | is always equicontinuous (cf. [[Equicontinuity|Equicontinuity]]). |
| | | | |
| − | A semi-group is said to be equicontinuous (of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140315.png" />) if the family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140316.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140317.png" />, is equicontinuous. | + | A semi-group is said to be equicontinuous (of class $ uC _ {0} $) |
| | + | if the family $ T ( t ) $, |
| | + | $ 0 \leq t < \infty $, |
| | + | is equicontinuous. |
| | | | |
| | Infinitesimal operators and infinitesimal generators are defined as in the Banach space case. | | Infinitesimal operators and infinitesimal generators are defined as in the Banach space case. |
| | | | |
| − | Assume from now on that the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140318.png" /> is sequentially complete. The infinitesimal generator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140319.png" /> of a semi-group of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140320.png" /> is identical to the infinitesimal operator; its domain of definition, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140321.png" />, is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140322.png" /> and, moreover, the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140323.png" /> is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140324.png" />. The semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140325.png" /> leaves <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140326.png" /> invariant and | + | Assume from now on that the space $ X $ |
| | + | is sequentially complete. The infinitesimal generator $ A $ |
| | + | of a semi-group of class $ l C _ {0} $ |
| | + | is identical to the infinitesimal operator; its domain of definition, $ D ( A) $, |
| | + | is dense in $ X $ |
| | + | and, moreover, the set $ \cap _ {n=} 1 ^ \infty D ( A ^ {n} ) $ |
| | + | is dense in $ X $. |
| | + | The semi-group $ T ( t ) $ |
| | + | leaves $ D ( A) $ |
| | + | invariant and |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140327.png" /></td> </tr></table>
| + | $$ |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140328.png" /> is the infinitesimal generator of a semi-group of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140329.png" />, the resolvent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140330.png" /> is defined for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140331.png" /> and is the Laplace transform of the semi-group.
| + | \frac{dT}{dt} |
| | + | ( t) x = \ |
| | + | AT ( t ) x = T ( t ) Ax ,\ 0 \leq t < \infty ,\ x \in D ( A ) . |
| | + | $$ |
| | | | |
| − | A linear operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140332.png" /> is the infinitesimal generator of a semi-group of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140333.png" /> if and only if it is closed, has dense domain of definition in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140334.png" />, and if there exists a sequence of positive numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140335.png" /> such that, for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140336.png" />, the resolvent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140337.png" /> is defined and the family of operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140338.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140339.png" /> is equicontinuous. In this situation the semi-group can be constructed by the formula | + | If $ A $ |
| | + | is the infinitesimal generator of a semi-group of class $ u C _ {0} $, |
| | + | the resolvent $ R ( \lambda , A ) $ |
| | + | is defined for $ \mathop{\rm Re} \lambda > 0 $ |
| | + | and is the Laplace transform of the semi-group. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140340.png" /></td> </tr></table>
| + | A linear operator $ A $ |
| | + | is the infinitesimal generator of a semi-group of class $ u C _ {0} $ |
| | + | if and only if it is closed, has dense domain of definition in $ X $, |
| | + | and if there exists a sequence of positive numbers $ \lambda _ {k} \rightarrow \infty $ |
| | + | such that, for any $ \lambda _ {k} $, |
| | + | the resolvent $ R ( \lambda _ {k} , A ) $ |
| | + | is defined and the family of operators $ [ \lambda _ {k} R ( \lambda _ {k} , A ) ] ^ {n} $, |
| | + | $ k , n = 1 , 2 \dots $ |
| | + | is equicontinuous. In this situation the semi-group can be constructed by the formula |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140341.png" /></td> </tr></table>
| + | $$ |
| | + | ( t ) x = \lim\limits _ {k \rightarrow \infty } \ |
| | + | \left ( \mathop{\rm exp} \left [ - \lambda _ {k} - \lambda _ {k} ^ {2} R ( \lambda _ {k} , A ) \right ] t \right ) x , |
| | + | $$ |
| | | | |
| − | In a non-normed locally convex space, the infinitesimal generator of a semi-group of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140342.png" /> may have no resolvent at any point. An example is: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140343.png" /> in the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140344.png" /> of infinitely-differentiable functions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140345.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140346.png" />. As a substitute for the resolvent one can take a continuous operator whose product with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140347.png" />, from the right and the left, differs by a "small amount" from the identity operator.
| + | $$ |
| | + | t \geq 0 ,\ x \in X . |
| | + | $$ |
| | | | |
| − | A continuous operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140348.png" /> defined for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140349.png" /> in a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140350.png" /> is called an asymptotic resolvent for a linear operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140351.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140352.png" /> is continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140353.png" />, the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140354.png" /> can be extended from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140355.png" /> to a continuous operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140356.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140357.png" />, and if there exists a limit point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140358.png" /> of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140359.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140360.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140361.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140362.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140363.png" />, where
| + | In a non-normed locally convex space, the infinitesimal generator of a semi-group of class $ lC _ {0} $ |
| | + | may have no resolvent at any point. An example is: $ A = d / ds $ |
| | + | in the space $ C ^ \infty $ |
| | + | of infinitely-differentiable functions of $ s $ |
| | + | on $ \mathbf R $. |
| | + | As a substitute for the resolvent one can take a continuous operator whose product with $ A - \lambda I $, |
| | + | from the right and the left, differs by a "small amount" from the identity operator. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140364.png" /></td> </tr></table>
| + | A continuous operator $ R ( \lambda ) $ |
| | + | defined for $ \lambda $ |
| | + | in a set $ \Lambda \subset \mathbf C $ |
| | + | is called an asymptotic resolvent for a linear operator $ A $ |
| | + | if $ AR ( \lambda ) $ |
| | + | is continuous on $ X $, |
| | + | the operator $ R ( \lambda ) A $ |
| | + | can be extended from $ D ( A) $ |
| | + | to a continuous operator $ B ( \lambda ) $ |
| | + | on $ X $, |
| | + | and if there exists a limit point $ \lambda _ {0} $ |
| | + | of the set $ \Lambda $ |
| | + | such that $ H ^ {+} ( \lambda ) x \rightarrow 0 $, |
| | + | $ H ^ {-} ( \lambda ) x \rightarrow 0 $ |
| | + | as $ \lambda \rightarrow \lambda _ {0} $ |
| | + | for any $ x \in X $, |
| | + | where |
| | + | |
| | + | $$ |
| | + | H ^ {+} ( \lambda ) = ( A - \lambda I ) R ( \lambda ) - I ,\ \ |
| | + | H ^ {-} ( \lambda ) = B ( \lambda ) - \lambda R ( \lambda ) - I . |
| | + | $$ |
| | | | |
| | An asymptotic resolvent possesses various properties resembling those of the ordinary resolvent. | | An asymptotic resolvent possesses various properties resembling those of the ordinary resolvent. |
| | | | |
| − | A closed linear operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140365.png" /> with a dense domain of definition in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140366.png" /> is the infinitesimal generator of a semi-group of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140367.png" /> if and only if there exist numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140368.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140369.png" /> such that, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140370.png" />, there exists an asymptotic resolvent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140371.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140372.png" /> with the properties: the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140373.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140374.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140375.png" /> are strongly infinitely differentiable for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140376.png" />, and the families of operators | + | A closed linear operator $ A $ |
| | + | with a dense domain of definition in $ X $ |
| | + | is the infinitesimal generator of a semi-group of class $ l C _ {0} $ |
| | + | if and only if there exist numbers $ \omega $ |
| | + | and $ \alpha > 0 $ |
| | + | such that, for $ \lambda > \omega $, |
| | + | there exists an asymptotic resolvent $ R ( \lambda ) $ |
| | + | of $ A $ |
| | + | with the properties: the functions $ R ( \lambda ) $, |
| | + | $ H ^ {+} ( \lambda ) $, |
| | + | $ H ^ {-} ( \lambda ) $ |
| | + | are strongly infinitely differentiable for $ \lambda > \omega $, |
| | + | and the families of operators |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140377.png" /></td> </tr></table>
| + | $$ |
| | + | e ^ {\alpha \lambda } |
| | + | \frac{d ^ {n} H ^ \pm ( \lambda ) }{d \lambda |
| | + | ^ {n} } |
| | + | ,\ |
| | + | \frac{\lambda ^ {n+} 1 }{n ! } |
| | + | |
| | + | \frac{d ^ {n} R ( \lambda ) }{d \lambda ^ {n} } |
| | + | ,\ \lambda > \omega ,\ n = 0 , 1 \dots |
| | + | $$ |
| | | | |
| | are equicontinuous. | | are equicontinuous. |
| Line 223: |
Line 681: |
| | | | |
| | ==Adjoint semi-groups.== | | ==Adjoint semi-groups.== |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140378.png" /> is a semi-group of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140379.png" /> on a Banach space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140380.png" />, then the adjoint operators form a semi-group of bounded operators on the adjoint space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140381.png" />. However, the assertion that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140382.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140383.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140384.png" /> is valid only in the sense of the weak- topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140385.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140386.png" /> is the generating operator, its adjoint <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140387.png" /> is a weak infinitesimal generator for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140388.png" />, in the sense that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140389.png" /> is the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140390.png" /> for which the limit of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140391.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140392.png" /> exists in the sense of weak- convergence and is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140393.png" />. The domain of definition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140394.png" /> is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140395.png" /> — again in the sense of the weak- topology — and the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140396.png" /> is closed in the weak- topology. | + | If $ T ( t ) $ |
| | + | is a semi-group of class $ C _ {0} $ |
| | + | on a Banach space $ X $, |
| | + | then the adjoint operators form a semi-group of bounded operators on the adjoint space $ X ^ \prime $. |
| | + | However, the assertion that $ T ^ \prime ( t ) f \rightarrow f $ |
| | + | as $ t \rightarrow 0 $ |
| | + | for any $ f \in X ^ \prime $ |
| | + | is valid only in the sense of the weak- topology $ \sigma ( X ^ \prime , X ) $. |
| | + | If $ A $ |
| | + | is the generating operator, its adjoint $ A ^ \prime $ |
| | + | is a weak infinitesimal generator for $ T ^ \prime ( t ) $, |
| | + | in the sense that $ D ( A ^ \prime ) $ |
| | + | is the set of all $ f $ |
| | + | for which the limit of $ t ^ {-} 1 [ T ^ \prime ( t ) - I ] f $ |
| | + | as $ t\rightarrow 0 $ |
| | + | exists in the sense of weak- convergence and is equal to $ A ^ \prime f $. |
| | + | The domain of definition $ D ( A ^ \prime ) $ |
| | + | is dense in $ X ^ \prime $— |
| | + | again in the sense of the weak- topology — and the operator $ A ^ \prime $ |
| | + | is closed in the weak- topology. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140397.png" /> be the set of all elements in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140398.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140399.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140400.png" /> in the strong sense; then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140401.png" /> is a closed subspace of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140402.png" /> that is invariant under all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140403.png" />. On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140404.png" /> the operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140405.png" /> form a semi-group of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140406.png" />. The space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140407.png" /> is also the strong closure of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140408.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140409.png" />. If the original space is reflexive, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140410.png" />. Analogous propositions hold for semi-groups of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140411.png" /> in locally convex spaces. Semi-groups of classes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140412.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140413.png" /> generate semi-groups of the same classes in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140414.png" />. | + | Let $ X ^ {+} $ |
| | + | be the set of all elements in $ X ^ \prime $ |
| | + | such that $ T ^ \prime ( f ) \rightarrow f $ |
| | + | as $ t \rightarrow 0 $ |
| | + | in the strong sense; then $ X ^ {+} $ |
| | + | is a closed subspace of $ X ^ \prime $ |
| | + | that is invariant under all $ T ^ \prime ( t ) $. |
| | + | On $ X ^ {+} $ |
| | + | the operators $ T ^ \prime ( t ) $ |
| | + | form a semi-group of class $ C _ {0} $. |
| | + | The space $ X ^ {+} $ |
| | + | is also the strong closure of the set $ D ( A ^ \prime ) $ |
| | + | in $ X ^ \prime $. |
| | + | If the original space is reflexive, then $ X ^ {+} = X ^ \prime $. |
| | + | Analogous propositions hold for semi-groups of class $ C _ {0} $ |
| | + | in locally convex spaces. Semi-groups of classes $ l C _ {0} $ |
| | + | and $ u C _ {0} $ |
| | + | generate semi-groups of the same classes in $ X ^ {+} $. |
| | | | |
| | ==Distribution semi-groups in a (separable) locally convex space.== | | ==Distribution semi-groups in a (separable) locally convex space.== |
| − | A distribution semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140415.png" /> in a sequentially complete locally convex space is defined just as in a Banach space. A semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140416.png" /> is said to be locally equicontinuous (of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140419.png" />) if, for any compact subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140420.png" />, the family of operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140421.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140422.png" />, is equicontinuous. In a barrelled space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140423.png" />, any distribution semi-group is defined by analogy to the Banach case. For semi-groups of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140424.png" />, the infinitesimal operator is closed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140425.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140426.png" /> is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140427.png" />, and for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140428.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140429.png" />, | + | A distribution semi-group $ T $ |
| | + | in a sequentially complete locally convex space is defined just as in a Banach space. A semi-group $ T $ |
| | + | is said to be locally equicontinuous (of class $ lD ^ \prime $) |
| | + | if, for any compact subset $ K \subset D ( \mathbf R ) $, |
| | + | the family of operators $ \{ T ( \phi ) \} $, |
| | + | $ \phi \in K $, |
| | + | is equicontinuous. In a barrelled space $ X $, |
| | + | any distribution semi-group is defined by analogy to the Banach case. For semi-groups of class $ l D ^ \prime $, |
| | + | the infinitesimal operator is closed $ ( A _ {0} = A ) $, |
| | + | $ \cap _ {n=} 1 ^ \infty D ( A ^ {n} ) $ |
| | + | is dense in $ X $, |
| | + | and for any $ x \in X $ |
| | + | and $ \phi \in D ( \mathbf R ) $, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140430.png" /></td> <td valign="top" style="width:5%;text-align:right;">(7)</td></tr></table>
| + | $$ \tag{7 } |
| | + | \left . |
| | + | \begin{array}{c} |
| | | | |
| − | A generalized function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140431.png" /> with support in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140432.png" />, possessing the properties (7), is naturally called the fundamental function of the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140434.png" />. Thus, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140435.png" /> is the infinitesimal operator of a semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140436.png" /> of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140437.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140438.png" /> is the fundamental function of the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140439.png" />. The converse statement is true under certain additional assumptions about the order of singularity of the fundamental function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140440.png" /> (or, more precisely, of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140441.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140442.png" />). | + | {T ( \phi ) x \in D ( A ) ,\ |
| | + | T ^ \prime ( \phi ) x = AT ( \phi ) x + \phi ( 0 ) x , } |
| | + | \\ |
| | | | |
| − | A useful notion for the characterization of semi-groups in a locally convex space is that of the generalized resolvent. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140443.png" /> denote the Laplace transform of a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140444.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140445.png" /> be the space of all such transforms. A topology is induced in this space, via the Laplace transform, from the topology of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140446.png" />. The Laplace transform of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140447.png" />-valued generalized function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140448.png" /> is defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140449.png" />. Under these conditions, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140450.png" /> is a continuous mapping of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140451.png" /> into the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140452.png" /> of continuous linear operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140453.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140454.png" /> be the space of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140455.png" /> obtained from functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140456.png" /> with support in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140457.png" />, with the natural topology. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140458.png" /> is a linear operator on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140459.png" />, it can be "lifted" to an operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140460.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140461.png" /> via the equality
| + | {T ^ \prime ( \phi ) x = T ( \phi ) Ax + \phi ( 0 ) x ,\ x \in D ( A ). } |
| | + | \end{array} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140462.png" /></td> </tr></table>
| + | \right \} |
| | + | $$ |
| | | | |
| − | Thus, it is defined for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140463.png" /> such that the right-hand side of the equality is defined for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140464.png" /> and it extends to a generalized function in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140465.png" />. The continuous operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140466.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140467.png" /> is defined by
| + | A generalized function $ T $ |
| | + | with support in $ [ 0 , \infty ) $, |
| | + | possessing the properties (7), is naturally called the fundamental function of the operator $ ( d / dt ) - A $. |
| | + | Thus, if $ A $ |
| | + | is the infinitesimal operator of a semi-group $ T $ |
| | + | of class $ l D ^ \prime $, |
| | + | then $ T $ |
| | + | is the fundamental function of the operator $ ( d / dt ) - A $. |
| | + | The converse statement is true under certain additional assumptions about the order of singularity of the fundamental function $ T $( |
| | + | or, more precisely, of the function $ f ( T ( \phi ) x ) $, |
| | + | where $ f \in X ^ \prime $). |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140468.png" /></td> </tr></table>
| + | A useful notion for the characterization of semi-groups in a locally convex space is that of the generalized resolvent. Let $ \widehat \phi $ |
| | + | denote the Laplace transform of a function $ \phi \in D ( \mathbf R ) $, |
| | + | and let $ \widehat{D} ( \mathbf R ) $ |
| | + | be the space of all such transforms. A topology is induced in this space, via the Laplace transform, from the topology of $ D ( \mathbf R ) $. |
| | + | The Laplace transform of an $ X $- |
| | + | valued generalized function $ F $ |
| | + | is defined by $ \widehat{F} ( \widehat \phi ) = F ( \phi ) $. |
| | + | Under these conditions, $ \widehat{F} $ |
| | + | is a continuous mapping of $ \widehat{D} ( \mathbf R ) $ |
| | + | into the space $ L ( X ) $ |
| | + | of continuous linear operators on $ X $. |
| | + | Let $ \widehat{D} {} _ {+} ^ \prime $ |
| | + | be the space of all $ \widehat{F} $ |
| | + | obtained from functions $ F $ |
| | + | with support in $ ( 0 , \infty ) $, |
| | + | with the natural topology. If $ A $ |
| | + | is a linear operator on $ X $, |
| | + | it can be "lifted" to an operator $ \widetilde{A} $ |
| | + | on $ \widehat{D} {} _ {+} ^ \prime $ |
| | + | via the equality |
| | | | |
| − | If the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140469.png" /> has a continuous inverse <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140470.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140471.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140472.png" /> is called the generalized resolvent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140473.png" />.
| + | $$ |
| | + | ( \widetilde{A} \widehat{F} ) = A ( \widehat{F} ( \widehat \phi ) ) = A F ( \phi ) . |
| | + | $$ |
| | | | |
| − | An operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140474.png" /> has a generalized resolvent if and only if the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140475.png" /> has a locally equicontinuous fundamental function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140476.png" />, constructed by the formula
| + | Thus, it is defined for all $ \widehat{F} \in \widehat{D} {} _ {+} ^ \prime $ |
| | + | such that the right-hand side of the equality is defined for any $ \phi \in D ( \mathbf R ) $ |
| | + | and it extends to a generalized function in $ \widehat{D} {} _ {+} ^ \prime $. |
| | + | The continuous operator $ \widetilde \lambda $ |
| | + | on $ \widehat{D} {} _ {+} ^ \prime $ |
| | + | is defined by |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140477.png" /></td> </tr></table>
| + | $$ |
| | + | ( \widetilde \lambda \widehat{F} ) ( \widehat \phi ) = \lambda \widehat{F} ( \widehat \phi ) = F ^ \prime |
| | + | ( \phi ) = - F ( \phi ^ \prime ) . |
| | + | $$ |
| | + | |
| | + | If the operator $ \widetilde{A} - \widetilde \lambda $ |
| | + | has a continuous inverse $ \widetilde{R} $ |
| | + | on $ \widehat{D} {} _ {+} ^ \prime $, |
| | + | then $ \widetilde{R} $ |
| | + | is called the generalized resolvent of $ A $. |
| | + | |
| | + | An operator $ A $ |
| | + | has a generalized resolvent if and only if the operator $ ( d / dt ) - A $ |
| | + | has a locally equicontinuous fundamental function $ T $, |
| | + | constructed by the formula |
| | + | |
| | + | $$ |
| | + | T ( \phi ) x = ( \widetilde{R} ( 1 \otimes x ) ) ( \widehat \phi ) ,\ \phi \in D ( \mathbf R ) ,\ \ |
| | + | x \in X , |
| | + | $$ |
| | | | |
| | where | | where |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140478.png" /></td> </tr></table>
| + | $$ |
| | + | ( 1 \otimes x ) ( \widehat \phi ) = ( \delta \otimes x ) \phi = \phi ( 0 ) x . |
| | + | $$ |
| | | | |
| − | Subject to certain additional assumptions, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140479.png" /> is a distribution semi-group. An extension theorem for semi-groups of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140480.png" /> has also been proved in terms of generalized resolvents. | + | Subject to certain additional assumptions, $ T $ |
| | + | is a distribution semi-group. An extension theorem for semi-groups of class $ l C _ {0} $ |
| | + | has also been proved in terms of generalized resolvents. |
| | | | |
| | See also [[Semi-group of non-linear operators|Semi-group of non-linear operators]]. | | See also [[Semi-group of non-linear operators|Semi-group of non-linear operators]]. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Yu.M. Vuvunikyan, "Evolutionary representations of algebras of generalized functions" , ''Theory of operators in function spaces'' , Novosibirsk (1977) pp. 99–120 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.P. Zabreiko, A.V. Zafievskii, "On a certain class of semigroups" ''Soviet Math. Dokl.'' , '''10''' : 6 (1969) pp. 1523–1526 ''Dokl. Akad. Nauk SSSR'' , '''189''' : 5 (1969) pp. 934–937</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.V. Zafievskii, ''Trudy Mat. Inst. Voronezh. Univ.'' , '''1''' (1970) pp. 206–210</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, §1</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> S.G. Krein, "Linear differential equations in Banach space" , ''Transl. Math. Monogr.'' , '''29''' , Amer. Math. Soc. (1971) (Translated from Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> Yu.T. Sil'chenko, "An evolutionary equation with an operator generating a nonlinear semigroup" ''Differential Equations'' , '''15''' : 2 (1979) pp. 255–258 ''Differentsial'nye Uravneniya'' , '''15''' : 2 (1979) pp. 363–366</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> J. Chazarain, "Problèmes de Cauchy abstracts et applications à quelques problèmes mixtes" ''J. Funct. Anal.'' , '''7''' : 3 (1971) pp. 386–446</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> I. Ciorânescu, "La caracterisation spectrale d'opérateur, générateurs des semi-groupes distributions d'ordre fini de croissance" ''J. Math. Anal. Appl.'' , '''34''' (1971) pp. 34–41</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> I. Ciorânescu, "A characterization of distribution semigroups of finite growth order" ''Rev. Roum. Math. Pures Appl.'' , '''22''' : 8 (1977) pp. 1053–1068</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> T. Kato, "A characterization of holomorphic semigroups" ''Proc. Amer. Math. Soc.'' , '''25''' : 3 (1970) pp. 495–498</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> J. Lions, "Les semigroupes distributions" ''Portugal. Math.'' , '''19''' (1960) pp. 141–164</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> A. Pazy, "On the differentiability and compactness of semi-groups of linear operators" ''J. Math. Mech.'' , '''17''' : 12 (1968) pp. 1131–1141</TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> A. Pazy, "Approximations of the identity operator by semigroups of linear operators" ''Proc. Amer. Math. Soc.'' , '''30''' : 1 (1971) pp. 147–150</TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> T. Ushijima, "On the abstract Cauchy problems and semi-groups of linear operators in locally convex spaces" ''Sci. Papers College Gen. Educ. Univ. Tokyo'' , '''21''' (1971) pp. 93–122</TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> T. Ushijima, "On the generation and smoothness of semi-groups of linear operators" ''J. Fac. Sci. Univ. Tokyo, Sec. 1A'' , '''19''' : 1 (1972) pp. 65–127</TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> C. Wild, "Semi-groupes de croissance <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140481.png" /> holomorphes" ''C.R. Acad. Sci. Paris Sér. A'' , '''285''' (1977) pp. 437–440 (English abstract)</TD></TR><TR><TD valign="top">[18]</TD> <TD valign="top"> J.A. Gol'dstein, "Semigroups of linear operators and application" , Oxford Univ. Press (1985) (Translated from Russian)</TD></TR><TR><TD valign="top">[19]</TD> <TD valign="top"> A. Pazy, "Semigroups of linear operators and application to partial differential equations" , Springer (1983)</TD></TR><TR><TD valign="top">[20]</TD> <TD valign="top"> Ph. Clément, H.J.A.M. Heijmans, S. Angenent, C.J. van Duijn, B. de Pagter, "One-parameter semigroups" , ''CWI Monographs'' , '''5''' , North-Holland (1987)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) {{MR|0089373}} {{ZBL|0392.46001}} {{ZBL|0033.06501}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Yu.M. Vuvunikyan, "Evolutionary representations of algebras of generalized functions" , ''Theory of operators in function spaces'' , Novosibirsk (1977) pp. 99–120 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.P. Zabreiko, A.V. Zafievskii, "On a certain class of semigroups" ''Soviet Math. Dokl.'' , '''10''' : 6 (1969) pp. 1523–1526 ''Dokl. Akad. Nauk SSSR'' , '''189''' : 5 (1969) pp. 934–937 {{MR|264459}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.V. Zafievskii, ''Trudy Mat. Inst. Voronezh. Univ.'' , '''1''' (1970) pp. 206–210</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, §1 {{MR|0617913}} {{ZBL|0435.46002}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> S.G. Krein, "Linear differential equations in Banach space" , ''Transl. Math. Monogr.'' , '''29''' , Amer. Math. Soc. (1971) (Translated from Russian) {{MR|0342804}} {{ZBL|0179.20701}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> Yu.T. Sil'chenko, "An evolutionary equation with an operator generating a nonlinear semigroup" ''Differential Equations'' , '''15''' : 2 (1979) pp. 255–258 ''Differentsial'nye Uravneniya'' , '''15''' : 2 (1979) pp. 363–366 {{MR|}} {{ZBL|0505.34046}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> J. Chazarain, "Problèmes de Cauchy abstracts et applications à quelques problèmes mixtes" ''J. Funct. Anal.'' , '''7''' : 3 (1971) pp. 386–446</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> I. Ciorânescu, "La caracterisation spectrale d'opérateur, générateurs des semi-groupes distributions d'ordre fini de croissance" ''J. Math. Anal. Appl.'' , '''34''' (1971) pp. 34–41</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> I. Ciorânescu, "A characterization of distribution semigroups of finite growth order" ''Rev. Roum. Math. Pures Appl.'' , '''22''' : 8 (1977) pp. 1053–1068 {{MR|500280}} {{ZBL|0374.46032}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> T. Kato, "A characterization of holomorphic semigroups" ''Proc. Amer. Math. Soc.'' , '''25''' : 3 (1970) pp. 495–498 {{MR|0264456}} {{ZBL|0199.45604}} </TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> J. Lions, "Les semigroupes distributions" ''Portugal. Math.'' , '''19''' (1960) pp. 141–164</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> A. Pazy, "On the differentiability and compactness of semi-groups of linear operators" ''J. Math. Mech.'' , '''17''' : 12 (1968) pp. 1131–1141 {{MR|231242}} {{ZBL|0162.45903}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> A. Pazy, "Approximations of the identity operator by semigroups of linear operators" ''Proc. Amer. Math. Soc.'' , '''30''' : 1 (1971) pp. 147–150 {{MR|0287362}} {{ZBL|}} </TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> T. Ushijima, "On the abstract Cauchy problems and semi-groups of linear operators in locally convex spaces" ''Sci. Papers College Gen. Educ. Univ. Tokyo'' , '''21''' (1971) pp. 93–122 {{MR|0312324}} {{ZBL|0239.47031}} </TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> T. Ushijima, "On the generation and smoothness of semi-groups of linear operators" ''J. Fac. Sci. Univ. Tokyo, Sec. 1A'' , '''19''' : 1 (1972) pp. 65–127 {{MR|0308854}} {{ZBL|0239.47032}} </TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> C. Wild, "Semi-groupes de croissance <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140481.png" /> holomorphes" ''C.R. Acad. Sci. Paris Sér. A'' , '''285''' (1977) pp. 437–440 (English abstract) {{MR|448159}} {{ZBL|0359.47024}} </TD></TR><TR><TD valign="top">[18]</TD> <TD valign="top"> J.A. Gol'dstein, "Semigroups of linear operators and application" , Oxford Univ. Press (1985) (Translated from Russian)</TD></TR><TR><TD valign="top">[19]</TD> <TD valign="top"> A. Pazy, "Semigroups of linear operators and application to partial differential equations" , Springer (1983) {{MR|0710486}} {{ZBL|}} </TD></TR><TR><TD valign="top">[20]</TD> <TD valign="top"> Ph. Clément, H.J.A.M. Heijmans, S. Angenent, C.J. van Duijn, B. de Pagter, "One-parameter semigroups" , ''CWI Monographs'' , '''5''' , North-Holland (1987) {{MR|0915552}} {{ZBL|0636.47051}} </TD></TR></table> |
| − | | |
| − | | |
| | | | |
| | ====Comments==== | | ====Comments==== |
| − |
| |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P. Butzer, H. Berens, "Semigroups of operators and approximation" , Springer (1967)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H. Kellermann, M. Hieber, "Integrated semigroups" ''J. Funct. Anal.'' , '''84''' (1989) pp. 160–180</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> I. Miyadera, N. Tanaka, "Exponentially bounded <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140482.png" />-semigroups and integrated semigroups" ''Tokyo J. Math.'' , '''12''' (1989) pp. 99–115</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P. Butzer, H. Berens, "Semigroups of operators and approximation" , Springer (1967) {{MR|230022}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H. Kellermann, M. Hieber, "Integrated semigroups" ''J. Funct. Anal.'' , '''84''' (1989) pp. 160–180 {{MR|0999494}} {{ZBL|0604.47025}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> I. Miyadera, N. Tanaka, "Exponentially bounded <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084140/s084140482.png" />-semigroups and integrated semigroups" ''Tokyo J. Math.'' , '''12''' (1989) pp. 99–115 {{MR|1001735}} {{ZBL|}} </TD></TR></table> |
A family $ \{ T \} $
of operators on a Banach space or topological vector space with the property that the composite of any two operators in the family is again a member of the family. If the operators $ T $
are "indexed" by elements of some abstract semi-group $ \mathfrak A $
and the binary operation of the latter is compatible with the composition of operators, $ \{ T \} $
is known as a representation of the semi-group $ \mathfrak A $.
The most detailed attention has been given to one-parameter semi-groups (cf. One-parameter semi-group) of bounded linear operators on a Banach space $ X $,
which yield a representation of the additive semi-group of all positive real numbers, i.e. families $ T ( t) $
with the property
$$
T ( t + \tau ) x = T ( t) T ( \tau ) x ,\ t , \tau > 0 ,\ x \in X .
$$
If $ T ( t) $
is strongly measurable, $ t > 0 $,
then $ T ( t) $
is a strongly-continuous semi-group; this will be assumed in the sequel.
The limit
$$
\omega = \lim\limits _ {t \rightarrow \infty } \
t ^ {-} 1 \mathop{\rm ln} \| T ( t) \|
$$
exists; it is known as the type of the semi-group. The functions $ T ( t) x $
increase at most exponentially.
An important characteristic is the infinitesimal operator (infinitesimal generator) of the semi-group:
$$
A _ {0} x = \lim\limits _ {t \rightarrow 0 } t ^ {-} 1 [ T ( t) x - x ] ,
$$
defined on the linear set $ D ( A _ {0} ) $
of all elements $ x $
for which the limit exists; the closure, $ A $,
of this operator (if it exists) is known as the generating operator, or generator, of the semi-group. Let $ X _ {0} $
be the subspace defined as the closure of the union of all values $ T ( t) x $;
then $ D ( A _ {0} ) $
is dense in $ X _ {0} $.
If there are no non-zero elements in $ X _ {0} $
such that $ T ( t) x \equiv 0 $,
then the generating operator $ A $
exists. In the sequel it will be assumed that $ X _ {0} = X $
and that $ T ( t) x \equiv 0 $
implies $ x = 0 $.
The simplest class of semi-groups, denoted by $ C _ {0} $,
is defined by the condition: $ T ( t) x \rightarrow x $
as $ t \rightarrow 0 $
for any $ x \in X $.
This is equivalent to the condition: The function $ \| T ( t) \| $
is bounded on any interval $ ( 0 , a ] $.
In that case $ T ( t) $
has a generating operator $ A = A _ {0} $
whose resolvent $ R ( \lambda , A ) = ( A - \lambda I ) ^ {-} 1 $
satisfies the inequalities
$$ \tag{1 }
\| R ^ {n} ( \lambda , A ) \| \leq M ( \lambda - \omega ) ^ {-} n ,\ \
n = 1 , 2 , . . . ; \ \lambda > \omega ,
$$
where $ \omega $
is the type of the semi-group. Conversely, if $ A $
is a closed operator with domain of definition dense in $ X $
and with a resolvent satisfying (1), then it is the generating operator of some semi-group $ T ( t) $
of class $ C _ {0} $
such that $ \| T ( t) \| \leq M e ^ {\omega t } $.
Condition (1) is satisfied if
$$
\| R ( \lambda , A ) \| \leq ( \lambda - \omega ) ^ {-} 1
$$
(the Hill–Yosida condition). If, moreover, $ \omega = 0 $,
then $ T ( t) $
is a contraction semi-group: $ \| T ( t) \| \leq 1 $.
A summable semi-group is a semi-group for which the functions $ \| T ( t) x \| $
are summable on any finite interval for all $ x \in X $.
A summable semi-group has a generating operator $ A = \overline{ {A _ {0} }}\; $.
The operator $ A _ {0} $
is closed if and only if, for every $ x \in X $,
$$
\lim\limits _ {t \rightarrow 0 }
\frac{1}{t}
\int\limits _ { 0 } ^ { t } T ( s) x d s = x .
$$
For $ \mathop{\rm Re} \lambda > \omega $
one can define the Laplace transform of a summable semi-group,
$$ \tag{2 }
\int\limits _ { 0 } ^ \infty e ^ {- \lambda t } T ( t)
x d t = - R ( \lambda ) x ,
$$
giving a bounded linear operator $ R ( \lambda ) $
which has many properties of a resolvent operator.
A closed operator $ A $
with domain of definition dense in $ X $
is the generating operator of a summable semi-group $ T ( t) $
if and only if, for some $ \omega $,
the resolvent $ R ( \lambda , A ) $
exists for $ \mathop{\rm Re} \lambda > \omega $
and the following conditions hold: a) $ \| R ( \lambda , A ) \| \leq M $,
$ \mathop{\rm Re} \lambda > \omega $;
b) there exist a non-negative function $ \phi ( t , x ) $,
$ t > 0 $,
$ x \in X $,
jointly continuous in all its variables, and a non-negative function $ \phi ( t) $,
bounded on any interval $ [ a , b ] \subset ( 0 , \infty ) $,
such that, for $ \omega _ {1} > \omega $,
$$
\int\limits _ { 0 } ^ \infty e ^ {- \omega _ {1} t } \phi ( t , x ) dt < \infty ,
$$
$$
\overline{\lim\limits}\; _ {t \rightarrow \infty } t ^ {-} 1 \mathop{\rm ln} \phi ( t) < \infty
,\ \phi ( t , x ) \leq \phi ( t) \| x \| ,
$$
$$
\| R ^ {n} ( \lambda , A ) x \| \leq
\frac{1}{
( n - 1 ) ! }
\int\limits _ { 0 } ^ \infty t ^ {n-} 1 e ^ {- \lambda t } \phi ( t , x ) dt .
$$
Under these conditions
$$
\| T ( t) x \| \leq \phi ( t , x ) ,\ \
\| T ( t) \| \leq \phi ( t) .
$$
If one requires in addition that the function $ \| T ( t) \| $
be summable on finite intervals, a necessary and sufficient condition is the existence of a continuous function $ \phi ( t) $
such that, for $ \omega _ {1} > \omega $,
$$ \tag{3 }
\int\limits _ { 0 } ^ \infty \phi ( t) e ^ {- \omega _ {1} t } dt < \infty ,
$$
$$ \tag{4 }
\| R ^ {n} ( \lambda , A ) \| \leq
\frac{1}{( n - 1
) ! }
\int\limits _ { 0 } ^ \infty t ^ {n-} 1 e ^ {- \lambda t } \phi ( t) dt ,
$$
$$
\lambda > \omega ,\ n= 1 , 2 , . . . .
$$
Under these conditions, $ \| T ( t) \| \leq \phi ( t) $.
By choosing different functions satisfying (3), one can define different subclasses of summable semi-groups. If $ \phi ( t) = Me ^ {\omega t } $,
the result is the class $ C _ {0} $
and (1) follows from (4). If $ \phi ( t) = Mt ^ {- \alpha } e ^ {\omega t } $,
$ 0 \leq \alpha < 1 $,
condition (4) implies the condition
$$
\| R ^ {n} ( \lambda , A ) \| \leq
\frac{M \Gamma ( n - \alpha ) }{( n - 1 ) ! ( \lambda - \omega ) ^ {n - \alpha } }
,\ \
\lambda > \omega ,\ n = 1 , 2 ,\dots.
$$
Semi-groups with power singularities.
If in the previous example $ \alpha \geq 1 $,
then the integrals in (4) are divergent for $ n \leq \alpha - 1 $.
Hence the generating operator for the corresponding semi-group may not have a resolvent for any $ \lambda $,
i.e. it may have a spectrum equal to the entire complex plane. However, for $ n $
large enough one can define for such operators functions $ S _ {n} ( \lambda , A ) $
which coincide with the functions $ R ^ {n+} 1 ( \lambda , A ) $
in the previous cases. The operator function $ S _ {n} ( \lambda , A ) $
is called a resolvent of order $ n $
if it is analytic in some domain $ G \subset \mathbf C $
and if for $ \lambda \in G $,
$$
S _ {n} ( \lambda , A ) Ax = A S _ {n} ( \lambda , A ) x ,\ \
x \in D ( A) ,
$$
$$
S _ {n} ( \lambda , A ) ( A - \lambda ) ^ {n+} 1 x = x ,\ x \in D ( A ^ {n+} 1 ) ,
$$
and if $ S _ {n} ( \lambda , A ) x = 0 $
for all $ \lambda \in G $
implies $ x = 0 $.
If $ \overline{D}\; ( A ^ {n+} 1 ) = X $,
the operator may have a unique resolvent of order $ n $,
for which there is a maximal domain of analyticity, known as the resolvent set of order $ n $.
Let $ T ( t) $
be a strongly-continuous semi-group such that the inequality
$$
\| T ( t) \| \leq M t ^ {- \alpha } e ^ {\omega t }
$$
holds for $ \alpha \geq 1 $.
Then its generating operator $ B $
has a resolvent of order $ n $
for $ n > \alpha - 1 $,
and, moreover,
$$
S _ {n} ( \lambda , B ) x = \
\frac{1}{n!}
\int\limits _ { 0 } ^ \infty t ^ {n} e ^ {- \lambda t } T
( t) x dt ,\ \mathop{\rm Re} \lambda > \omega ,
$$
$$ \tag{5 }
\left \|
\frac{d ^ {k} S _ {n} ( \lambda , B ) }{d \lambda ^ {k} }
x \right \| \leq
\frac{M \Gamma ( k + n + 1 - \alpha ) }{n
! ( \mathop{\rm Re} \lambda - \omega ) ^ {k + n + 1 - \alpha } }
,
$$
$$
\mathop{\rm Re} \lambda > \omega ,\ k = 0 , 1 ,\dots .
$$
Conversely, suppose that for $ \mathop{\rm Re} \lambda > 0 $
the operator $ B $
has a resolvent $ S _ {n} ( \lambda , B ) $
of order $ n $
satisfying (5) with $ n > \alpha - 1 $.
Then there exists a unique semi-group $ T ( t) $
such that
$$
\| T ( t) \| \leq M t ^ {- \alpha } e ^ {\omega t } ,
$$
and the generating operator $ A $
of this semi-group is such that $ S _ {n} ( \lambda , A ) = S _ {n} ( \lambda , B ) $.
Smooth semi-groups.
If $ x \in D ( A _ {0} ) $,
the function $ T ( t) x $
is continuously differentiable and
$$
\frac{d T ( t) }{dt}
x = A _ {0} T
( t) x = T ( t) A _ {0} x .
$$
There exist semi-groups of class $ C _ {0} $
such that, if $ x \notin D ( A _ {0} ) = D ( A) $,
the functions $ T ( t) x $
are non-differentiable for all $ t $.
However, there are important classes of semi-groups for which the degree of smoothness increases with increasing $ t $.
If the functions $ T ( t) x $,
$ t > t _ {0} $,
are differentiable for any $ x \in X $,
then it follows from the semi-group property that the $ T ( t) x $
are twice differentiable if $ t > 2 t _ {0} $,
three times differentiable if $ t > 3 t _ {0} $,
etc. Therefore, if these functions are differentiable at any $ t > 0 $
for $ x \in X $,
then $ T ( t) x $
is infinitely differentiable.
Given a semi-group of class $ C _ {0} $,
a necessary and sufficient condition for the functions $ T ( t) x $
to be differentiable for all $ x \in X $
and $ t > t _ {0} $,
where $ t _ {0} \geq 0 $,
is that there exist numbers $ a , b , c > 0 $
such that the resolvent $ R ( \lambda , A ) $
is defined in the domain
$$
\mathop{\rm Re} \lambda > a - b \mathop{\rm ln} | \mathop{\rm Im} \lambda | ,
$$
while in this domain
$$
\| R( \lambda , A ) \| \leq c | \mathop{\rm Im} \lambda | .
$$
A necessary and sufficient condition for $ T ( t) x $
to be infinitely differentiable for all $ x \in X $
and $ t > 0 $
is that, for every $ b > 0 $,
there exist $ a _ {b} , c _ {b} $
such that the resolvent $ R ( \lambda , A ) $
is defined in the domain
$$
\mathop{\rm Re} \lambda > a _ {b} - b \mathop{\rm ln} | \mathop{\rm Im} \lambda | ,
$$
and such that
$$
\| R ( \lambda , A ) \| \leq c _ {b} | \mathop{\rm Im} \lambda | .
$$
Sufficient conditions are: If there exists a $ \mu > \omega $
for which
$$
\overline{\lim\limits}\; _ {\tau \rightarrow \infty } \mathop{\rm ln} | \tau | \| R ( \mu + i \tau , A ) \| = t _ {0} < \infty ,
$$
then the $ T ( t) x $
are differentiable for $ t > t _ {0} $
and $ x \in X $;
if $ t _ {0} = 0 $,
then the $ T ( t) x $
are infinitely differentiable for all $ t > 0 $
and $ x \in X $.
The degree of smoothness of a semi-group may sometimes be inferred from its behaviour at zero; for example, suppose that for every $ c > 0 $
there exists a $ \delta _ {c} $
such that, for $ 0 < t < \delta _ {c} $,
$$
\| I - T ( t) \| \leq 2 - ct \mathop{\rm ln} t ^ {-} 1 ,
$$
then the $ T ( t) x $
are infinitely differentiable for all $ t > 0 $,
$ x \in X $.
There are smoothness conditions for summable semi-groups and semi-groups of polynomial growth. If a semi-group has polynomial growth of degree $ \alpha $
and is infinitely differentiable for $ t > 0 $,
then the function
$$
\frac{d T ( t) }{dt}
x = A T ( t) x
$$
also has polynomial growth:
$$
\| A T ( t) \| \leq M _ {1} t ^ {- \beta } e ^ {\omega t } .
$$
In the general case there is no rigorous relationship between the numbers $ \alpha $
and $ \beta $,
and $ \beta $
can be utilized for a more detailed classification of infinitely-differentiable semi-groups of polynomial growth.
Analytic semi-groups.
An important class of semi-groups, related to partial differential equations of parabolic type, comprises those semi-groups $ T ( t) $
which admit an analytic continuation to some sector of the complex plane containing the positive real axis. A semi-group of class $ C _ {0} $
has this property if and only if its resolvent satisfies the following inequality in some right half-plane $ \mathop{\rm Re} \lambda > \omega $:
$$
\| R ( \lambda , A ) \| \leq M | \lambda - \omega | ^ {-} 1 .
$$
Another necessary and sufficient conditions is: The semi-group is strongly differentiable and its derivative satisfies the estimate
$$
\left \|
\frac{d T }{dt}
( t) \right \| \leq M t ^ {-} 1 e ^ {\omega t } .
$$
Finally, the inequality
$$
\overline{\lim\limits}\; _ {t \rightarrow 0 } \| I - T ( t) \| < 2
$$
is also a sufficient condition for $ T ( t) $
to be analytic.
If a semi-group $ T ( t) $
has an analytic continuation $ T ( z) $
to a sector $ | \mathop{\rm arg} z | < \phi \leq \pi / 2 $
and has polynomial growth at zero, $ \| T ( z) \| \leq c | z | ^ \alpha $,
$ \alpha > 0 $,
then the resolvent $ S _ {n} ( \lambda , A ) $
of order $ n > \alpha - 1 $
of its generating operator $ A $
has an analytic continuation to the sector $ | \mathop{\rm arg} \lambda | \leq \pi / 2 + \phi $,
and satisfies the following estimate in any sector $ | \mathop{\rm arg} \lambda | \leq \pi / 2 + \psi $,
$ \psi < \phi $:
$$
\| S _ {n} ( \lambda , A ) \| \leq | \lambda | ^
{\alpha - n - 1 } M ( \psi ) .
$$
Conversely, suppose that the resolvent $ S _ {n} ( \lambda , B ) $
of an operator $ B $
is defined in a sector $ | \mathop{\rm arg} \lambda | \leq \pi / 2 + \psi $
and that
$$
\| S _ {n} ( \lambda , B ) \| \leq \lambda ^ {\alpha - n - 1 } M .
$$
Then there exists a semi-group $ T ( z) $
of growth $ \alpha $,
analytic in the sector $ | \mathop{\rm arg} z | < \psi $,
whose generating operator $ A $
is such that $ S _ {n} ( \lambda , A ) = S _ {n} ( \lambda , B ) $.
Distribution semi-groups.
In accordance with the general concept of the theory of distributions (cf. Generalized function), one can drop the requirement that the operator-valued function $ T ( t) $
be defined for every $ t > 0 $,
demanding only that it be possible to evaluate the integrals $ \int _ {- \infty } ^ {+ \infty } T ( t) \phi ( t) dt $
for all $ \phi $
in the space $ D ( \mathbf R ) $
of infinitely-differentiable functions with compact support. Hence the following definition: A distribution semi-group on a Banach space $ X $
is a continuous linear mapping $ T ( \phi ) $
of $ D ( \mathbf R ) $
into the space $ L ( X) $
of all bounded linear operators on $ X $,
with the following properties: a) $ T ( \phi ) = 0 $
if $ \supp \phi \subset ( - \infty , 0 ) $;
b) if $ \phi , \psi $
are functions in the subspace $ D ^ {+} ( \mathbf R ) $
of all functions in $ D ( \mathbf R ) $
with support in $ ( 0 , \infty ) $,
then $ T ( \phi * \psi ) = T ( \phi ) T ( \psi ) $,
where the star denotes convolution:
$$
\phi * \psi = \int\limits _ {- \infty } ^ \infty \phi ( t - s ) \psi ( s) d s
$$
(the semi-group property); c) if $ T ( \phi ) x = 0 $
for all $ \phi \in D ^ {+} ( \mathbf R ) $,
then $ x = 0 $;
d) the linear hull of the set of all values of $ T ( \phi ) x $,
$ \phi \in D ^ {+} ( \mathbf R ) $,
$ x \in X $,
is dense in $ X $;
e) for any $ y = T ( \psi ) x $,
$ \psi \in D ^ {+} ( \mathbf R ) $,
there exists a continuous $ u ( t) $
on $ ( 0 , \infty ) $
with values in $ X $,
so that $ u( 0) = y $
and
$$
T ( \phi ) y = \int\limits _ { 0 } ^ \infty \phi ( t) u ( t) dt
$$
for all $ \phi \in D ( \mathbf R ) $.
The infinitesimal operator $ A _ {0} $
of a distribution semi-group is defined as follows. If there exists a delta-sequence $ \{ \rho _ {n} \} \subset D ^ {+} ( \mathbf R ) $
such that $ T ( \rho _ {n} ) x \rightarrow x $
and $ T ( - \rho _ {n} ^ \prime ) x \rightarrow y $
as $ n \rightarrow \infty $,
then $ x \in D ( A _ {0} ) $
and $ y = A _ {0} x $.
The infinitesimal operator has a closure $ A = \overline{ {A _ {0} }}\; $,
known as the infinitesimal generator of the distribution semi-group. The set $ \cap _ {n=} 1 ^ \infty D ( A _ {0} ^ {n} ) $
is dense in $ X $
and contains $ T ( \phi ) X $
for any $ \phi \in D ^ {+} ( \mathbf R ) $.
A closed linear operator $ A $
with a dense domain of definition in $ X $
is the infinitesimal generator of a distribution semi-group if and only if there exist numbers $ a , b \geq 0 $,
$ c > 0 $
and a natural number $ m $
such that the resolvent $ R ( \lambda , A ) $
exists for $ \mathop{\rm Re} \lambda \geq a \mathop{\rm ln} ( 1 + | \lambda | ) + b $
and satisfies the inequality
$$ \tag{6 }
\| R ( \lambda , A ) \| \leq c ( 1 + | \lambda | ) ^ {m} .
$$
If $ A $
is a closed linear operator on $ X $,
then the set $ \cap _ {n=} 1 ^ \infty D ( A ^ {n} ) $
can be made into a Fréchet space $ X _ \infty $
by introducing the system of norms
$$
\| x \| _ {n} = \
\sum _ { k= } 0 ^ { n } \| A ^ {k} x \| .
$$
The restriction $ A _ \infty $
of $ A $
to $ X _ \infty $
leaves $ X _ \infty $
invariant. If $ A $
is the infinitesimal generator of a semi-group, then $ A _ \infty $
is the infinitesimal generator of a semi-group of class $ C _ {0} $(
continuous for $ t \geq 0 $,
$ T ( 0 ) = I $)
on $ X _ \infty $.
Conversely, if $ X _ \infty $
is dense in $ X $,
the operator $ A $
has a non-empty resolvent set and $ A $
is the infinitesimal generator of a semi-group of class $ C _ {0} $
on $ X _ \infty $,
then $ A $
is the infinitesimal generator of a distribution semi-group on $ X $.
A distribution semi-group has exponential growth of order at most $ q $,
$ 1 \leq q < \infty $,
if there exists an $ \omega > 0 $
such that $ \mathop{\rm exp} ( - \omega t ^ {q} ) T ( \phi ) $
is a continuous mapping in the topology induced on $ D ^ {+} $
by the space $ S ( \mathbf R ) $
of rapidly-decreasing functions. A closed linear operator is the infinitesimal generator of a distribution semi-group with the above property if and only if it has a resolvent $ R ( \lambda , A ) $
which satisfies (6) in the domain
$$
\{ \lambda : { \mathop{\rm Re} \lambda \geq [ \alpha \mathop{\rm ln} ( 1 + | \mathop{\rm Im} \
\lambda | + \beta ) ] ^ {1- 1/q } , \mathop{\rm Re} \lambda > \omega } \}
,
$$
where $ \alpha , \beta > 0 $.
In particular, if $ q = 1 $
the semi-group is said to be exponential and inequality (6) is valid in some half-plane. There exists a characterization of the semi-groups of the above types in terms of the operator $ A _ \infty $.
Questions of smoothness and analyticity have also been investigated for distribution semi-groups.
Semi-groups of operators in a (separable) locally convex space $ X $.
The definition of a strongly-continuous semi-group of operators $ T ( t ) $
continuous on $ X $
remains the same as for a Banach space. Similarly, the class $ C _ {0} $
is defined by the property $ T ( t ) x \rightarrow x $
as $ t \rightarrow 0 $
for any $ x \in X $.
A semi-group is said to be locally equicontinuous (of class $ lC _ {0} $)
if the family of operators $ T ( t ) $
is equicontinuous when $ t $
ranges over any finite interval in $ ( 0 , \infty ) $.
In a barrelled space, a semi-group of class $ C _ {0} $
is always equicontinuous (cf. Equicontinuity).
A semi-group is said to be equicontinuous (of class $ uC _ {0} $)
if the family $ T ( t ) $,
$ 0 \leq t < \infty $,
is equicontinuous.
Infinitesimal operators and infinitesimal generators are defined as in the Banach space case.
Assume from now on that the space $ X $
is sequentially complete. The infinitesimal generator $ A $
of a semi-group of class $ l C _ {0} $
is identical to the infinitesimal operator; its domain of definition, $ D ( A) $,
is dense in $ X $
and, moreover, the set $ \cap _ {n=} 1 ^ \infty D ( A ^ {n} ) $
is dense in $ X $.
The semi-group $ T ( t ) $
leaves $ D ( A) $
invariant and
$$
\frac{dT}{dt}
( t) x = \
AT ( t ) x = T ( t ) Ax ,\ 0 \leq t < \infty ,\ x \in D ( A ) .
$$
If $ A $
is the infinitesimal generator of a semi-group of class $ u C _ {0} $,
the resolvent $ R ( \lambda , A ) $
is defined for $ \mathop{\rm Re} \lambda > 0 $
and is the Laplace transform of the semi-group.
A linear operator $ A $
is the infinitesimal generator of a semi-group of class $ u C _ {0} $
if and only if it is closed, has dense domain of definition in $ X $,
and if there exists a sequence of positive numbers $ \lambda _ {k} \rightarrow \infty $
such that, for any $ \lambda _ {k} $,
the resolvent $ R ( \lambda _ {k} , A ) $
is defined and the family of operators $ [ \lambda _ {k} R ( \lambda _ {k} , A ) ] ^ {n} $,
$ k , n = 1 , 2 \dots $
is equicontinuous. In this situation the semi-group can be constructed by the formula
$$
( t ) x = \lim\limits _ {k \rightarrow \infty } \
\left ( \mathop{\rm exp} \left [ - \lambda _ {k} - \lambda _ {k} ^ {2} R ( \lambda _ {k} , A ) \right ] t \right ) x ,
$$
$$
t \geq 0 ,\ x \in X .
$$
In a non-normed locally convex space, the infinitesimal generator of a semi-group of class $ lC _ {0} $
may have no resolvent at any point. An example is: $ A = d / ds $
in the space $ C ^ \infty $
of infinitely-differentiable functions of $ s $
on $ \mathbf R $.
As a substitute for the resolvent one can take a continuous operator whose product with $ A - \lambda I $,
from the right and the left, differs by a "small amount" from the identity operator.
A continuous operator $ R ( \lambda ) $
defined for $ \lambda $
in a set $ \Lambda \subset \mathbf C $
is called an asymptotic resolvent for a linear operator $ A $
if $ AR ( \lambda ) $
is continuous on $ X $,
the operator $ R ( \lambda ) A $
can be extended from $ D ( A) $
to a continuous operator $ B ( \lambda ) $
on $ X $,
and if there exists a limit point $ \lambda _ {0} $
of the set $ \Lambda $
such that $ H ^ {+} ( \lambda ) x \rightarrow 0 $,
$ H ^ {-} ( \lambda ) x \rightarrow 0 $
as $ \lambda \rightarrow \lambda _ {0} $
for any $ x \in X $,
where
$$
H ^ {+} ( \lambda ) = ( A - \lambda I ) R ( \lambda ) - I ,\ \
H ^ {-} ( \lambda ) = B ( \lambda ) - \lambda R ( \lambda ) - I .
$$
An asymptotic resolvent possesses various properties resembling those of the ordinary resolvent.
A closed linear operator $ A $
with a dense domain of definition in $ X $
is the infinitesimal generator of a semi-group of class $ l C _ {0} $
if and only if there exist numbers $ \omega $
and $ \alpha > 0 $
such that, for $ \lambda > \omega $,
there exists an asymptotic resolvent $ R ( \lambda ) $
of $ A $
with the properties: the functions $ R ( \lambda ) $,
$ H ^ {+} ( \lambda ) $,
$ H ^ {-} ( \lambda ) $
are strongly infinitely differentiable for $ \lambda > \omega $,
and the families of operators
$$
e ^ {\alpha \lambda }
\frac{d ^ {n} H ^ \pm ( \lambda ) }{d \lambda
^ {n} }
,\
\frac{\lambda ^ {n+} 1 }{n ! }
\frac{d ^ {n} R ( \lambda ) }{d \lambda ^ {n} }
,\ \lambda > \omega ,\ n = 0 , 1 \dots
$$
are equicontinuous.
Generation theorems have also been proved for other classes of semi-groups of operators on a locally convex space.
Adjoint semi-groups.
If $ T ( t ) $
is a semi-group of class $ C _ {0} $
on a Banach space $ X $,
then the adjoint operators form a semi-group of bounded operators on the adjoint space $ X ^ \prime $.
However, the assertion that $ T ^ \prime ( t ) f \rightarrow f $
as $ t \rightarrow 0 $
for any $ f \in X ^ \prime $
is valid only in the sense of the weak- topology $ \sigma ( X ^ \prime , X ) $.
If $ A $
is the generating operator, its adjoint $ A ^ \prime $
is a weak infinitesimal generator for $ T ^ \prime ( t ) $,
in the sense that $ D ( A ^ \prime ) $
is the set of all $ f $
for which the limit of $ t ^ {-} 1 [ T ^ \prime ( t ) - I ] f $
as $ t\rightarrow 0 $
exists in the sense of weak- convergence and is equal to $ A ^ \prime f $.
The domain of definition $ D ( A ^ \prime ) $
is dense in $ X ^ \prime $—
again in the sense of the weak- topology — and the operator $ A ^ \prime $
is closed in the weak- topology.
Let $ X ^ {+} $
be the set of all elements in $ X ^ \prime $
such that $ T ^ \prime ( f ) \rightarrow f $
as $ t \rightarrow 0 $
in the strong sense; then $ X ^ {+} $
is a closed subspace of $ X ^ \prime $
that is invariant under all $ T ^ \prime ( t ) $.
On $ X ^ {+} $
the operators $ T ^ \prime ( t ) $
form a semi-group of class $ C _ {0} $.
The space $ X ^ {+} $
is also the strong closure of the set $ D ( A ^ \prime ) $
in $ X ^ \prime $.
If the original space is reflexive, then $ X ^ {+} = X ^ \prime $.
Analogous propositions hold for semi-groups of class $ C _ {0} $
in locally convex spaces. Semi-groups of classes $ l C _ {0} $
and $ u C _ {0} $
generate semi-groups of the same classes in $ X ^ {+} $.
Distribution semi-groups in a (separable) locally convex space.
A distribution semi-group $ T $
in a sequentially complete locally convex space is defined just as in a Banach space. A semi-group $ T $
is said to be locally equicontinuous (of class $ lD ^ \prime $)
if, for any compact subset $ K \subset D ( \mathbf R ) $,
the family of operators $ \{ T ( \phi ) \} $,
$ \phi \in K $,
is equicontinuous. In a barrelled space $ X $,
any distribution semi-group is defined by analogy to the Banach case. For semi-groups of class $ l D ^ \prime $,
the infinitesimal operator is closed $ ( A _ {0} = A ) $,
$ \cap _ {n=} 1 ^ \infty D ( A ^ {n} ) $
is dense in $ X $,
and for any $ x \in X $
and $ \phi \in D ( \mathbf R ) $,
$$ \tag{7 }
\left .
\begin{array}{c}
{T ( \phi ) x \in D ( A ) ,\
T ^ \prime ( \phi ) x = AT ( \phi ) x + \phi ( 0 ) x , }
\\
{T ^ \prime ( \phi ) x = T ( \phi ) Ax + \phi ( 0 ) x ,\ x \in D ( A ). }
\end{array}
\right \}
$$
A generalized function $ T $
with support in $ [ 0 , \infty ) $,
possessing the properties (7), is naturally called the fundamental function of the operator $ ( d / dt ) - A $.
Thus, if $ A $
is the infinitesimal operator of a semi-group $ T $
of class $ l D ^ \prime $,
then $ T $
is the fundamental function of the operator $ ( d / dt ) - A $.
The converse statement is true under certain additional assumptions about the order of singularity of the fundamental function $ T $(
or, more precisely, of the function $ f ( T ( \phi ) x ) $,
where $ f \in X ^ \prime $).
A useful notion for the characterization of semi-groups in a locally convex space is that of the generalized resolvent. Let $ \widehat \phi $
denote the Laplace transform of a function $ \phi \in D ( \mathbf R ) $,
and let $ \widehat{D} ( \mathbf R ) $
be the space of all such transforms. A topology is induced in this space, via the Laplace transform, from the topology of $ D ( \mathbf R ) $.
The Laplace transform of an $ X $-
valued generalized function $ F $
is defined by $ \widehat{F} ( \widehat \phi ) = F ( \phi ) $.
Under these conditions, $ \widehat{F} $
is a continuous mapping of $ \widehat{D} ( \mathbf R ) $
into the space $ L ( X ) $
of continuous linear operators on $ X $.
Let $ \widehat{D} {} _ {+} ^ \prime $
be the space of all $ \widehat{F} $
obtained from functions $ F $
with support in $ ( 0 , \infty ) $,
with the natural topology. If $ A $
is a linear operator on $ X $,
it can be "lifted" to an operator $ \widetilde{A} $
on $ \widehat{D} {} _ {+} ^ \prime $
via the equality
$$
( \widetilde{A} \widehat{F} ) = A ( \widehat{F} ( \widehat \phi ) ) = A F ( \phi ) .
$$
Thus, it is defined for all $ \widehat{F} \in \widehat{D} {} _ {+} ^ \prime $
such that the right-hand side of the equality is defined for any $ \phi \in D ( \mathbf R ) $
and it extends to a generalized function in $ \widehat{D} {} _ {+} ^ \prime $.
The continuous operator $ \widetilde \lambda $
on $ \widehat{D} {} _ {+} ^ \prime $
is defined by
$$
( \widetilde \lambda \widehat{F} ) ( \widehat \phi ) = \lambda \widehat{F} ( \widehat \phi ) = F ^ \prime
( \phi ) = - F ( \phi ^ \prime ) .
$$
If the operator $ \widetilde{A} - \widetilde \lambda $
has a continuous inverse $ \widetilde{R} $
on $ \widehat{D} {} _ {+} ^ \prime $,
then $ \widetilde{R} $
is called the generalized resolvent of $ A $.
An operator $ A $
has a generalized resolvent if and only if the operator $ ( d / dt ) - A $
has a locally equicontinuous fundamental function $ T $,
constructed by the formula
$$
T ( \phi ) x = ( \widetilde{R} ( 1 \otimes x ) ) ( \widehat \phi ) ,\ \phi \in D ( \mathbf R ) ,\ \
x \in X ,
$$
where
$$
( 1 \otimes x ) ( \widehat \phi ) = ( \delta \otimes x ) \phi = \phi ( 0 ) x .
$$
Subject to certain additional assumptions, $ T $
is a distribution semi-group. An extension theorem for semi-groups of class $ l C _ {0} $
has also been proved in terms of generalized resolvents.
See also Semi-group of non-linear operators.
References
| [1] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) MR0089373 Zbl 0392.46001 Zbl 0033.06501 |
| [2] | Yu.M. Vuvunikyan, "Evolutionary representations of algebras of generalized functions" , Theory of operators in function spaces , Novosibirsk (1977) pp. 99–120 (In Russian) |
| [3] | P.P. Zabreiko, A.V. Zafievskii, "On a certain class of semigroups" Soviet Math. Dokl. , 10 : 6 (1969) pp. 1523–1526 Dokl. Akad. Nauk SSSR , 189 : 5 (1969) pp. 934–937 MR264459 |
| [4] | A.V. Zafievskii, Trudy Mat. Inst. Voronezh. Univ. , 1 (1970) pp. 206–210 |
| [5] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, §1 MR0617913 Zbl 0435.46002 |
| [6] | S.G. Krein, "Linear differential equations in Banach space" , Transl. Math. Monogr. , 29 , Amer. Math. Soc. (1971) (Translated from Russian) MR0342804 Zbl 0179.20701 |
| [7] | Yu.T. Sil'chenko, "An evolutionary equation with an operator generating a nonlinear semigroup" Differential Equations , 15 : 2 (1979) pp. 255–258 Differentsial'nye Uravneniya , 15 : 2 (1979) pp. 363–366 Zbl 0505.34046 |
| [8] | J. Chazarain, "Problèmes de Cauchy abstracts et applications à quelques problèmes mixtes" J. Funct. Anal. , 7 : 3 (1971) pp. 386–446 |
| [9] | I. Ciorânescu, "La caracterisation spectrale d'opérateur, générateurs des semi-groupes distributions d'ordre fini de croissance" J. Math. Anal. Appl. , 34 (1971) pp. 34–41 |
| [10] | I. Ciorânescu, "A characterization of distribution semigroups of finite growth order" Rev. Roum. Math. Pures Appl. , 22 : 8 (1977) pp. 1053–1068 MR500280 Zbl 0374.46032 |
| [11] | T. Kato, "A characterization of holomorphic semigroups" Proc. Amer. Math. Soc. , 25 : 3 (1970) pp. 495–498 MR0264456 Zbl 0199.45604 |
| [12] | J. Lions, "Les semigroupes distributions" Portugal. Math. , 19 (1960) pp. 141–164 |
| [13] | A. Pazy, "On the differentiability and compactness of semi-groups of linear operators" J. Math. Mech. , 17 : 12 (1968) pp. 1131–1141 MR231242 Zbl 0162.45903 |
| [14] | A. Pazy, "Approximations of the identity operator by semigroups of linear operators" Proc. Amer. Math. Soc. , 30 : 1 (1971) pp. 147–150 MR0287362 |
| [15] | T. Ushijima, "On the abstract Cauchy problems and semi-groups of linear operators in locally convex spaces" Sci. Papers College Gen. Educ. Univ. Tokyo , 21 (1971) pp. 93–122 MR0312324 Zbl 0239.47031 |
| [16] | T. Ushijima, "On the generation and smoothness of semi-groups of linear operators" J. Fac. Sci. Univ. Tokyo, Sec. 1A , 19 : 1 (1972) pp. 65–127 MR0308854 Zbl 0239.47032 |
| [17] | C. Wild, "Semi-groupes de croissance 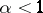 holomorphes" C.R. Acad. Sci. Paris Sér. A , 285 (1977) pp. 437–440 (English abstract) MR448159 Zbl 0359.47024 holomorphes" C.R. Acad. Sci. Paris Sér. A , 285 (1977) pp. 437–440 (English abstract) MR448159 Zbl 0359.47024 |
| [18] | J.A. Gol'dstein, "Semigroups of linear operators and application" , Oxford Univ. Press (1985) (Translated from Russian) |
| [19] | A. Pazy, "Semigroups of linear operators and application to partial differential equations" , Springer (1983) MR0710486 |
| [20] | Ph. Clément, H.J.A.M. Heijmans, S. Angenent, C.J. van Duijn, B. de Pagter, "One-parameter semigroups" , CWI Monographs , 5 , North-Holland (1987) MR0915552 Zbl 0636.47051 |
References
| [a1] | P. Butzer, H. Berens, "Semigroups of operators and approximation" , Springer (1967) MR230022 |
| [a2] | H. Kellermann, M. Hieber, "Integrated semigroups" J. Funct. Anal. , 84 (1989) pp. 160–180 MR0999494 Zbl 0604.47025 |
| [a3] | I. Miyadera, N. Tanaka, "Exponentially bounded  -semigroups and integrated semigroups" Tokyo J. Math. , 12 (1989) pp. 99–115 MR1001735 -semigroups and integrated semigroups" Tokyo J. Math. , 12 (1989) pp. 99–115 MR1001735 |
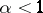 holomorphes" C.R. Acad. Sci. Paris Sér. A , 285 (1977) pp. 437–440 (English abstract) MR448159 Zbl 0359.47024
holomorphes" C.R. Acad. Sci. Paris Sér. A , 285 (1977) pp. 437–440 (English abstract) MR448159 Zbl 0359.47024  -semigroups and integrated semigroups" Tokyo J. Math. , 12 (1989) pp. 99–115 MR1001735
-semigroups and integrated semigroups" Tokyo J. Math. , 12 (1989) pp. 99–115 MR1001735