Semi-direct product
of a group  by a group
by a group 
A group  which is the product of its subgroups
which is the product of its subgroups  and
and  , where
, where  is normal in
is normal in  and
and  . If
. If  is also normal in
is also normal in 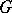 , then the semi-direct product becomes a direct product. The semi-direct product of two groups
, then the semi-direct product becomes a direct product. The semi-direct product of two groups 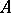 and
and 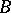 is not uniquely determined. To construct a semi-direct product one should also know which automorphisms of the group
is not uniquely determined. To construct a semi-direct product one should also know which automorphisms of the group  are induced by conjugation by elements of
are induced by conjugation by elements of  . More precisely, if
. More precisely, if  is a semi-direct product, then to each element
is a semi-direct product, then to each element 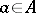 corresponds an automorphism
corresponds an automorphism 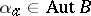 , which is conjugation by the element
, which is conjugation by the element  :
:
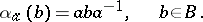 |
Here, the correspondence 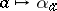 is a homomorphism
is a homomorphism  . Conversely, if
. Conversely, if 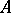 and
and  are arbitrary groups, then for any homomorphism
are arbitrary groups, then for any homomorphism 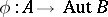 there is a unique semi-direct product of the group
there is a unique semi-direct product of the group 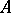 by the group
by the group 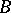 for which
for which 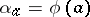 for any
for any 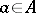 . A semi-direct product is a particular case of an extension of a group
. A semi-direct product is a particular case of an extension of a group  by a group
by a group  (cf. Extension of a group); such an extension is called split.
(cf. Extension of a group); such an extension is called split.
References
| [1] | A.G. Kurosh, "The theory of groups" , 1 , Chelsea (1960) (Translated from Russian) |
Comments
The semi-direct product of  by
by 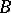 is often denoted by
is often denoted by 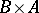 or
or 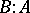 .
.
Semi-direct product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-direct_product&oldid=11367