Semi-definite form
A quadratic form  over an ordered field which represents either only non-negative field elements or only non-positive field elements. In the former case the form is said to be a non-negative definite (
over an ordered field which represents either only non-negative field elements or only non-positive field elements. In the former case the form is said to be a non-negative definite ( for all
for all  ), in the latter case — a non-positive definite quadratic form (
), in the latter case — a non-positive definite quadratic form ( ). Most frequently one considers semi-definite forms over the field
). Most frequently one considers semi-definite forms over the field  of real numbers. For the field
of real numbers. For the field  a similar definition yields the concept of (non-negative and non-positive) semi-definite Hermitian quadratic forms (see Hermitian form).
a similar definition yields the concept of (non-negative and non-positive) semi-definite Hermitian quadratic forms (see Hermitian form).
If  is a symmetric bilinear (cf. Bilinear form) or Hermitian form such that
is a symmetric bilinear (cf. Bilinear form) or Hermitian form such that  is a semi-definite form, then
is a semi-definite form, then  is sometimes also called a (non-negative or non-positive) semi-definite form. If
is sometimes also called a (non-negative or non-positive) semi-definite form. If  is a quadratic or Hermitian semi-definite form in a vector space
is a quadratic or Hermitian semi-definite form in a vector space 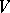 , then
, then 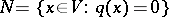 is a subspace, identical with the kernel of
is a subspace, identical with the kernel of 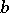 , and the given form naturally induces a positive-definite or negative-definite form on
, and the given form naturally induces a positive-definite or negative-definite form on  .
.
Comments
Instead of "non-negative definite" one also says positive semi-definite, and instead of "non-positive definite" also negative semi-definite.
Semi-definite form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-definite_form&oldid=11755