Semi-continuous summation method
A summation method (cf. Summation methods) for series and sequences, defined by means of sequences of functions. Let 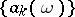 ,
, 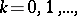 be a sequence of functions defined on some set
be a sequence of functions defined on some set 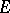 of variation of the parameter
of variation of the parameter 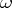 , and let
, and let 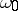 be an accumulation point of
be an accumulation point of 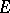 (finite or infinite). The functions
(finite or infinite). The functions  are used to convert a given sequence
are used to convert a given sequence 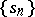 into a function
into a function 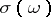 :
:
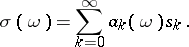 | (1) |
If the series in (1) is convergent for all  sufficiently close to
sufficiently close to 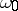 , and if
, and if
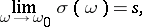 |
one says that the sequence 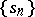 is summable to
is summable to  by the semi-continuous summation method defined by the sequence
by the semi-continuous summation method defined by the sequence 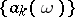 . If
. If 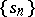 is the sequence of partial sums of the series
is the sequence of partial sums of the series
 | (2) |
one says that the series (2) is summable by the semi-continuous method to  . A semi-continuous summation method with
. A semi-continuous summation method with 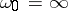 is an analogue of the matrix summation method defined by the matrix
is an analogue of the matrix summation method defined by the matrix 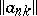 , in which the integer-valued parameter
, in which the integer-valued parameter  is replaced by the continuous parameter
is replaced by the continuous parameter 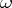 . The sequence of functions
. The sequence of functions 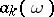 is therefore known as a semi-continuous matrix.
is therefore known as a semi-continuous matrix.
A semi-continuous summation method can be defined by direct transformation of a series into a function, using a given sequence of functions, say 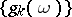 :
:
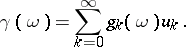 | (3) |
In this case the series (2) is said to be summable to  if
if
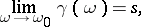 |
where 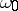 is an accumulation point of the set
is an accumulation point of the set 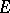 of variation of
of variation of 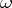 , and the series (3) is assumed to be convergent for all
, and the series (3) is assumed to be convergent for all 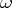 sufficiently close to
sufficiently close to 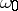 .
.
In some cases a semi-continuous summation method is more convenient than a summation method based on ordinary matrices, since it enables one to utilize tools of function theory. Examples of semi-continuous summation methods are: the Abel summation method, the Borel summation method, the Lindelöf summation method, and the Mittag-Leffler summation method. The class of semi-continuous methods also includes methods with semi-continuous matrices of the form
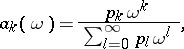 |
where the denominator is an entire function that does not reduce to a polynomial.
Conditions for the regularity of semi-continuous summation methods are analogous to regularity conditions for matrix summation methods. For example, the conditions
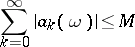 |
for all 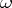 sufficiently close to
sufficiently close to 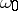 ,
,
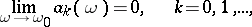 |
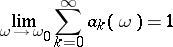 |
are necessary and sufficient for the semi-continuous summation method defined by the transformation (1) of 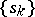 into a function to be regular (see Regularity criteria).
into a function to be regular (see Regularity criteria).
References
| [1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [2] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
| [3] | W. Beekmann, K. Zeller, "Theorie der Limitierungsverfahren" , Springer (1970) |
Semi-continuous summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-continuous_summation_method&oldid=48657