Difference between revisions of "Semi-algebraic set"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 5: | Line 5: | ||
A semi-analytic set is, by definition, a set in a real-analytic manifold which can be locally described by finitely many analytic equalities and inequalities. | A semi-analytic set is, by definition, a set in a real-analytic manifold which can be locally described by finitely many analytic equalities and inequalities. | ||
| − | The Tarski–Seidenberg theorem asserts the existence of a decision procedure (cf. also [[Decidable set|Decidable set]]) for deciding the truth of any elementary sentence built up from finitely many polynomial inequalities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s0839509.png" />, the connectives | + | The Tarski–Seidenberg theorem asserts the existence of a decision procedure (cf. also [[Decidable set|Decidable set]]) for deciding the truth of any elementary sentence built up from finitely many polynomial inequalities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s0839509.png" />, the connectives "and" , "or" and "not" , and the quantifiers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s08395010.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s08395011.png" />. Two precise formulations are: 1) Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s08395012.png" /> be a semi-algebraic set and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s08395013.png" /> the projection onto the last <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s08395014.png" /> coordinates. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s08395015.png" /> is semi-algebraic. 2) Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s08395016.png" /> be a finite sentence built up from inequalities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s08395017.png" /> and the connectives "and" , "or" and "not" (such a sentence is called a polynomial relation). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s08395018.png" /> be a series of quantifiers of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s08395019.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s08395020.png" />. There is an algorithm for finding a polynomial relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s08395021.png" /> such that |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s08395022.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083950/s08395022.png" /></td> </tr></table> | ||
| Line 20: | Line 20: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Hironaka, "Stratification and flatness" P. Holm (ed.) , ''Real and Complex Singularities (Oslo, 1976). Proc. Nordic Summer School'' , Sijthoff & Noordhoff (1977) pp. 199–266 {{MR|0499286}} {{ZBL|0424.32004}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Pawtucki, "Points de Nash des ensembles sous-analytiques" , Amer. Math. Soc. (1990)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G.W. Brumfiel, "Partially ordered rings and semi-algebraic geometry" , Cambridge Univ. Press (1979) {{MR|0553280}} {{ZBL|0415.13015}} </TD></TR></table> |
Revision as of 21:56, 30 March 2012
semi-analytic set.
A semi-algebraic set in 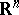 (or
(or 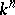 , where
, where 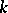 is a real closed field) is a set that can be given by finitely many polynomial equalities and inequalities. More precisely, for
is a real closed field) is a set that can be given by finitely many polynomial equalities and inequalities. More precisely, for 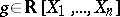 , let
, let 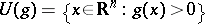 . Then
. Then 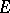 is semi-algebraic if it belongs to the smallest Boolean ring of subsets of
is semi-algebraic if it belongs to the smallest Boolean ring of subsets of 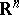 containing all the
containing all the 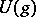 .
.
A semi-analytic set is, by definition, a set in a real-analytic manifold which can be locally described by finitely many analytic equalities and inequalities.
The Tarski–Seidenberg theorem asserts the existence of a decision procedure (cf. also Decidable set) for deciding the truth of any elementary sentence built up from finitely many polynomial inequalities 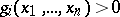 , the connectives "and" , "or" and "not" , and the quantifiers
, the connectives "and" , "or" and "not" , and the quantifiers 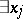 ,
, 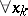 . Two precise formulations are: 1) Let
. Two precise formulations are: 1) Let 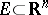 be a semi-algebraic set and
be a semi-algebraic set and 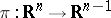 the projection onto the last
the projection onto the last 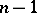 coordinates. Then
coordinates. Then 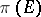 is semi-algebraic. 2) Let
is semi-algebraic. 2) Let 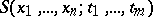 be a finite sentence built up from inequalities
be a finite sentence built up from inequalities 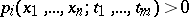 and the connectives "and" , "or" and "not" (such a sentence is called a polynomial relation). Let
and the connectives "and" , "or" and "not" (such a sentence is called a polynomial relation). Let 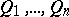 be a series of quantifiers of the form
be a series of quantifiers of the form 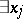 or
or 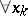 . There is an algorithm for finding a polynomial relation
. There is an algorithm for finding a polynomial relation  such that
such that
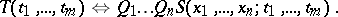 |
It follows from the Tarski–Seidenberg theorem that the image under a polynomial mapping 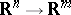 of a semi-algebraic set is semi-algebraic. Indeed, this is equivalent.
of a semi-algebraic set is semi-algebraic. Indeed, this is equivalent.
The image of a semi-analytic set under an analytic mapping is not necessarily semi-analytic. A subanalytic set on a real-analytic manifold is, by definition, a set that is locally the image of a semi-analytic set under an analytic mapping. The points of a subanalytic set at which it is not semi-analytic form a subanalytic set, cf. [a2].
The closure of a semi-algebraic (respectively, semi-analytic or subanalytic) set is again semi-algebraic (respectively, semi-analytic or subanalytic).
The image of a semi-algebraic (respectively, subanalytic) set under an algebraic (respectively, analytic) mapping is a semi-algebraic (respectively, subanalytic) set.
Finally, a semi-algebraic (respectively, semi-analytic or subanalytic) subset of a smooth algebraic (respectively, analytic or analytic) variety admits a smooth stratification, whose strata are semi-algebraic (respectively, semi-analytic or subanalytic) (and smooth).
References
| [a1] | H. Hironaka, "Stratification and flatness" P. Holm (ed.) , Real and Complex Singularities (Oslo, 1976). Proc. Nordic Summer School , Sijthoff & Noordhoff (1977) pp. 199–266 MR0499286 Zbl 0424.32004 |
| [a2] | W. Pawtucki, "Points de Nash des ensembles sous-analytiques" , Amer. Math. Soc. (1990) |
| [a3] | G.W. Brumfiel, "Partially ordered rings and semi-algebraic geometry" , Cambridge Univ. Press (1979) MR0553280 Zbl 0415.13015 |
Semi-algebraic set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-algebraic_set&oldid=11607