Segre characteristic of a square matrix
From Encyclopedia of Mathematics
Let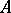 
be a square matrix over a field 
and let 
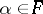, the algebraic closure of 
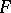, be an eigenvalue (cf. Eigen value) of 
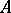. Over 
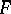the matrix 
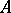can be put in Jordan normal form (see Jordan matrix). The Segre characteristic of 
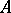at the eigenvalue 
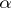is the sequence of sizes of the Jordan blocks of 
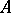with eigenvalue 
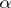in non-increasing order. The Segre characteristic of 
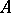consists of the complete set of data describing the Jordan normal form comprising all eigenvalues 
and the Segre characteristic of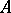 
at each of the 
.
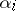References
| [a1] | H.W. Turnbull, A.C. Aitken, "An introduction to the theory of canonical matrices" , Blackie (1932) pp. Chapt. VI |
| [a2] | Ch.G. Cullen, "Matrices and linear transformations" , Addison-Wesley (1972) pp. Chap. 5 (Dover reprint, 1990) |
How to Cite This Entry:
Segre characteristic of a square matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Segre_characteristic_of_a_square_matrix&oldid=13050
Segre characteristic of a square matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Segre_characteristic_of_a_square_matrix&oldid=13050
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article