Segal-Shale-Weil representation
A representation of groups arising in both number theory and in physics. For number theorists, the seminal paper is that of A. Weil, [a1]. He cites earlier papers of I. Segal and D. Shale as precedents, and the deep work of C.L. Siegel on theta-series as inspiration.
Let  be a group with centre
be a group with centre  such that
such that  is Abelian, and let
is Abelian, and let  be a unitary character of
be a unitary character of  (cf. also Character of a group). If
(cf. also Character of a group). If  , choose representatives
, choose representatives  and note that
and note that  is independent of the choice of representatives. This is a skew-symmetric bilinear pairing
is independent of the choice of representatives. This is a skew-symmetric bilinear pairing  . One assumes that this pairing is non-degenerate. The Stone–von Neumann theorem asserts that
. One assumes that this pairing is non-degenerate. The Stone–von Neumann theorem asserts that 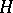 has a unique irreducible representation
has a unique irreducible representation  with central character
with central character 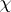 . Furthermore, the representation may be constructed as follows. Let
. Furthermore, the representation may be constructed as follows. Let 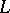 be a Lagrangian subgroup, that is, any subgroup of
be a Lagrangian subgroup, that is, any subgroup of  containing
containing 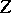 such that
such that 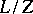 is a maximal subgroup of
is a maximal subgroup of 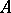 on which the form
on which the form 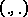 is trivial. Extend
is trivial. Extend  to
to 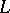 in an arbitrary manner, then induce. This gives a model for
in an arbitrary manner, then induce. This gives a model for  .
.
Let  be a group of automorphisms of
be a group of automorphisms of 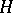 which acts trivially on
which acts trivially on  (cf. also Automorphism). If
(cf. also Automorphism). If  , the Stone–von Neumann theorem implies that
, the Stone–von Neumann theorem implies that  . Let
. Let 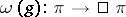 be an intertwining mapping, well defined up to constant multiple (cf. also Intertwining operator). Then
be an intertwining mapping, well defined up to constant multiple (cf. also Intertwining operator). Then  is a projective representation of
is a projective representation of 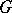 .
.
For example, let 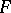 be a local field and let
be a local field and let  be a vector space over
be a vector space over 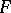 endowed with a non-degenerate skew-symmetric bilinear form
endowed with a non-degenerate skew-symmetric bilinear form  . Its dimension
. Its dimension 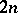 is even, and the automorphism group of the form is the symplectic group
is even, and the automorphism group of the form is the symplectic group  . One can construct a "Heisenberg group"
. One can construct a "Heisenberg group"  with the multiplication
with the multiplication 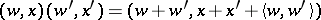 . Choosing any non-trivial additive character
. Choosing any non-trivial additive character  of
of  , let
, let  . Then the hypotheses of the Stone–von Neumann theorem are satisfied. As the Lagrangian subgroup of
. Then the hypotheses of the Stone–von Neumann theorem are satisfied. As the Lagrangian subgroup of  one may take
one may take  , where
, where 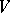 is any maximal isotropic subspace of
is any maximal isotropic subspace of 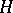 . Then the induced model of
. Then the induced model of 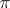 described above may be realized as the Schwartz space
described above may be realized as the Schwartz space  . The Segal–Shale–Weil representation is the resulting projective representation of
. The Segal–Shale–Weil representation is the resulting projective representation of 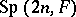 . It may be interpreted as a genuine representation of a covering group
. It may be interpreted as a genuine representation of a covering group 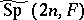 , the so-called metaplectic group.
, the so-called metaplectic group.
Now let  be a global field,
be a global field, 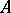 its adèle ring (cf. also Adèle), and let
its adèle ring (cf. also Adèle), and let 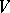 and
and 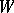 be as before. Then one may construct a similar representation
be as before. Then one may construct a similar representation 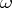 of
of 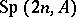 on the Schwartz space
on the Schwartz space 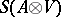 . If
. If  , let
, let  . This linear form is invariant under the action of
. This linear form is invariant under the action of  , generalizing the Poisson summation formula. This implies that the representation
, generalizing the Poisson summation formula. This implies that the representation  is automorphic. The corresponding automorphic forms are theta-functions (cf. Theta-function), having their historical origins in the work of C.G.J. Jacobi and Siegel. As Weil observed, the automorphicity of this representation is closely related to the quadratic reciprocity law.
is automorphic. The corresponding automorphic forms are theta-functions (cf. Theta-function), having their historical origins in the work of C.G.J. Jacobi and Siegel. As Weil observed, the automorphicity of this representation is closely related to the quadratic reciprocity law.
Later authors, notably R. Howe [a2], have emphasized the theory of dual reductive pairs. When a pair of reductive groups  embeds in
embeds in 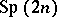 , each being the centralizer of the other (cf. also Centralizer), then
, each being the centralizer of the other (cf. also Centralizer), then 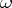 sets up a correspondence between representations of
sets up a correspondence between representations of  and representations of
and representations of 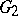 . This works at the level of automorphic forms and gives instances of Langlands functoriality, including some historically important ones such as quadratic base change (cf. also Base change). See [a3]. The use of the Weil representation in [a4] to construct automorphic forms and representations may be understood as arising from the dual reductive pairs
. This works at the level of automorphic forms and gives instances of Langlands functoriality, including some historically important ones such as quadratic base change (cf. also Base change). See [a3]. The use of the Weil representation in [a4] to construct automorphic forms and representations may be understood as arising from the dual reductive pairs 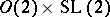 and
and 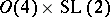 . The dual pair
. The dual pair  underlies the important work of J.-L. Waldspurger [a5] on automorphic forms of half-integral weight.
underlies the important work of J.-L. Waldspurger [a5] on automorphic forms of half-integral weight.
In recent years (as of 2000) it has been noted that since the Segal–Shale–Weil representation is the minimal representation of 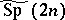 , that is, the representation with smallest Gel'fand–Kirillov dimension, minimal representations of other groups can play a similar role. Many interesting examples may be found in the exceptional groups (cf. also Lie algebra, exceptional). The possibly first paper where this phenomenon was noted was [a6]. Many interesting examples come from the exceptional groups. There is much current literature on this subject, but for typical papers see [a7] and [a8]. Dual pairs in the exceptional groups were classified in [a9].
, that is, the representation with smallest Gel'fand–Kirillov dimension, minimal representations of other groups can play a similar role. Many interesting examples may be found in the exceptional groups (cf. also Lie algebra, exceptional). The possibly first paper where this phenomenon was noted was [a6]. Many interesting examples come from the exceptional groups. There is much current literature on this subject, but for typical papers see [a7] and [a8]. Dual pairs in the exceptional groups were classified in [a9].
For further references see [a10].
References
| [a1] | A. Weil, "Sur certains groupes d'opérateurs unitaires" Acta Math. , 111 (1964) pp. 143–211 (Also: Collected Works, Vol. 3) |
| [a2] | R.E. Howe, " -series and invariant theory" , Automorphic forms, representations and -series and invariant theory" , Automorphic forms, representations and  -functions , Proc. Symp. Pure Math. , 33:1 , Amer. Math. Soc. (1977) -functions , Proc. Symp. Pure Math. , 33:1 , Amer. Math. Soc. (1977) |
| [a3] | S. Rallis, "Langlands' functoriality and the Weil representation" Amer. J. Math. , 104 : 3 (1982) pp. 469–515 |
| [a4] | H. Jacquet, R.P. Langlands, "Automorphic forms on 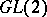 " , Lecture Notes in Mathematics , 114 , Springer (1970) " , Lecture Notes in Mathematics , 114 , Springer (1970) |
| [a5] | J.-L. Waldspurger, "Sur les coefficients de Fourier des formes modulaires de poids demi-entier" J. Math. Pures Appl. , 60 (1981) pp. 375–484 |
| [a6] | D. Kazhdan, "The minimal representation of 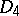 " , Operator Algebras, Unitary Representations, Enveloping Algebras, and Invariant Theory (Paris, 1989) , Birkhäuser (1990) pp. 125–158 " , Operator Algebras, Unitary Representations, Enveloping Algebras, and Invariant Theory (Paris, 1989) , Birkhäuser (1990) pp. 125–158 |
| [a7] | D. Ginzburg, S. Rallis, D. Soudry, "A tower of theta correspondences for 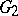 " Duke Math. J. , 88 (1997) pp. 537–624 " Duke Math. J. , 88 (1997) pp. 537–624 |
| [a8] | B.H. Gross, G. Savin, "The dual pair 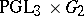 " Canad. Math. Bull. , 40 : 3 (1997) pp. 376–384 " Canad. Math. Bull. , 40 : 3 (1997) pp. 376–384 |
| [a9] | H. Rubenthaler, "Les paires duales dans les algèbres de Lie réductives" Astérisque , 219 (1994) |
| [a10] | D. Prasad, "A brief survey on the theta correspondence" , Number theory , Contemp. Math. , 210 , Amer. Math. Soc. (1998) pp. 171–193 |
Segal-Shale-Weil representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Segal-Shale-Weil_representation&oldid=12824