Sector in the theory of ordinary differential equations
An open curvilinear sector 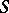 with vertex at an isolated singular point
with vertex at an isolated singular point 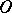 of an autonomous system of second-order ordinary differential equations
of an autonomous system of second-order ordinary differential equations
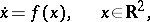 | (*) |
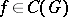 , where
, where 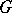 is the domain of uniqueness, that satisfies the following four conditions: 1) each lateral boundary of
is the domain of uniqueness, that satisfies the following four conditions: 1) each lateral boundary of 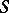 is a
is a 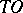 -curve of the system (*) (i.e. a semi-trajectory that approaches
-curve of the system (*) (i.e. a semi-trajectory that approaches 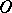 as
as 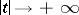 , and touches a certain direction at
, and touches a certain direction at 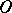 ); 2) the outer boundary of
); 2) the outer boundary of 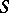 is a simple parametric arc (the homeomorphic image of a closed interval); 3)
is a simple parametric arc (the homeomorphic image of a closed interval); 3) 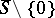 does not contain singular points of (*). The fourth condition is one of the following three: 4a) all trajectories of the system (*) that start in
does not contain singular points of (*). The fourth condition is one of the following three: 4a) all trajectories of the system (*) that start in 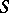 leave this sector for both increasing and decreasing
leave this sector for both increasing and decreasing 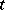 ; such a sector is called a hyperbolic sector, or a saddle sector (Fig. a); 4b) all trajectories of (*) that start in
; such a sector is called a hyperbolic sector, or a saddle sector (Fig. a); 4b) all trajectories of (*) that start in 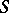 sufficiently near
sufficiently near  do not leave
do not leave 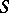 but approach
but approach 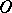 as
as 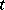 increases, and as
increases, and as 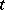 decreases they leave
decreases they leave 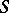 (or vice-versa); such a sector is called a parabolic sector or an open node sector (Fig. b); or 4c) all the trajectories of (*) that start in
(or vice-versa); such a sector is called a parabolic sector or an open node sector (Fig. b); or 4c) all the trajectories of (*) that start in 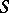 sufficiently near
sufficiently near 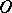 do not leave
do not leave 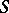 as
as 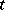 increases or decreases but approach
increases or decreases but approach 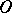 , forming together with
, forming together with 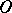 closed curves (loops), and for any two loops one encloses the other; such a sector is called an elliptic sector or a closed node sector (Fig. c).
closed curves (loops), and for any two loops one encloses the other; such a sector is called an elliptic sector or a closed node sector (Fig. c).

Figure: s083770a

Figure: s083770b

Figure: s083770c
For any analytic system (*) with 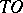 -curves, a disc
-curves, a disc 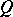 of sufficiently small radius and centre at
of sufficiently small radius and centre at 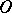 can always be divided into a finite number of sectors of a specific form:
can always be divided into a finite number of sectors of a specific form: 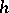 hyperbolic,
hyperbolic, 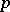 parabolic and
parabolic and  elliptic ones (see [1] and [2]). The Frommer method can be used to exhibit all these sectors, to determine the type of each, and to establish the rules of their succession in a circuit about
elliptic ones (see [1] and [2]). The Frommer method can be used to exhibit all these sectors, to determine the type of each, and to establish the rules of their succession in a circuit about 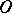 along the boundary of
along the boundary of 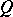 (and thereby to show the topological structure of the arrangement of the trajectories of (*) in a neighbourhood of
(and thereby to show the topological structure of the arrangement of the trajectories of (*) in a neighbourhood of 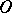 ). There are a priori estimates from above for
). There are a priori estimates from above for 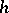 ,
, 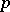 and
and  in terms of the order of smallness of the norm
in terms of the order of smallness of the norm 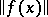 as
as 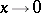 (see [1], [4], [5]).
(see [1], [4], [5]).
Sometimes (see, for example, [3]) the notion of a "sector" is defined more freely: In hyperbolic and parabolic sectors loops are allowed that cover a set without limit points on the rear boundary of a sector, and in elliptic sectors, loops that do not contain one another. Here the first sentence of the previous paragraph remains valid also for a system (*) of general form, and the Poincaré index 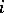 of the singular point
of the singular point 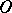 of (*) is expressed by Bendixson's formula
of (*) is expressed by Bendixson's formula
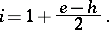 |
References
| [1] | I. Bendixson, "Sur des courbes définiés par des équations différentielles" Acta Math. , 24 (1901) pp. 1–88 |
| [2] | A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Qualitative theory of second-order dynamic systems" , Wiley (1973) (Translated from Russian) |
| [3] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
| [4] | A.N. Berlinskii, "On the structure of the neighborhood of a singular point of a two-dimensional autonomous system" Soviet Math. Dokl. , 10 : 4 (1969) pp. 882–885 Dokl. Akad. Nauk SSSR , 187 : 3 (1969) pp. 502–505 |
| [5] | M.E. Sagalovich, "Classes of local topological structures of an equilibrium state" Diff. Equations , 15 : 2 (1979) pp. 253–255 Differentsial'nye Urnveniya , 15 : 2 (1979) pp. 360–362 |
Comments
The lateral boundaries are sometimes called base solutions.
A Frommer sector, or Frommer normal domain, is a circular sector
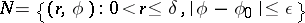 |
with vertex at an isolated point 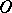 (
(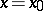 ) of the system
) of the system
(see 1)) with lateral boundary 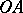 and
and 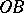 ,
, 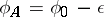 ,
, 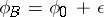 , and with the rear boundary
, and with the rear boundary 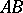 satisfying the following conditions (here
satisfying the following conditions (here  and
and 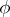 are polar coordinates in the
are polar coordinates in the  -plane with pole at
-plane with pole at 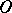 , and
, and 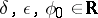 ):
):
A) 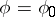 is an exceptional direction of the system
is an exceptional direction of the system
at 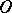 , that is, there is a sequence
, that is, there is a sequence 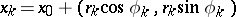 ,
, 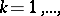
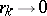 ,
, 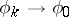 as
as 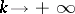 , such that if
, such that if 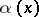 is the angle between the directions of the vectors
is the angle between the directions of the vectors  and
and 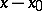 , then
, then 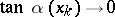 as
as 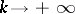 , and this direction is unique in
, and this direction is unique in 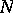 ;
;
B) 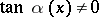 for any
for any 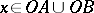 ;
;
C) 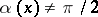 for any
for any 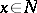 .
.
Suppose that the angle 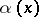 is measured from the vector
is measured from the vector 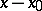 and has the sign of the reference direction. A sector
and has the sign of the reference direction. A sector 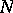 is called a Frommer normal domain of the first type (notation:
is called a Frommer normal domain of the first type (notation: 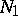 ) if
) if 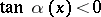 for
for 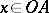 and
and 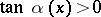 for
for 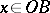 ; a normal domain of the second type (notation:
; a normal domain of the second type (notation: 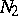 ) if
) if 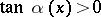 on
on 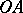 and
and 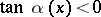 on
on 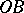 ; and a normal domain of the third type
; and a normal domain of the third type 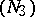 if
if 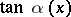 has one and the same sign on
has one and the same sign on 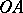 and on
and on 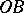 . These domains were introduced by M. Frommer [1].
. These domains were introduced by M. Frommer [1].
The trajectories of the system
in Frommer normal domains behave as follows. The domain 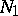 is covered by
is covered by 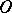 -curves of the system (Fig. d). They form an open pencil (cf. Sheaf 2)), that is, a family of
-curves of the system (Fig. d). They form an open pencil (cf. Sheaf 2)), that is, a family of 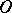 -curves of the same type that depends continuously on a parameter which varies over an open interval. In the domain
-curves of the same type that depends continuously on a parameter which varies over an open interval. In the domain 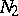 there is either a) a unique
there is either a) a unique 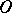 -curve (Fig. e), or b) infinitely many
-curve (Fig. e), or b) infinitely many 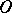 -curves (a closed pencil; cf. Fig. f). In the domain
-curves (a closed pencil; cf. Fig. f). In the domain 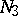 , either a) there are infinitely many
, either a) there are infinitely many  -curves (a semi-open pencil; Fig. g) or b) there are no
-curves (a semi-open pencil; Fig. g) or b) there are no 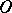 -curves (Fig. h).
-curves (Fig. h).
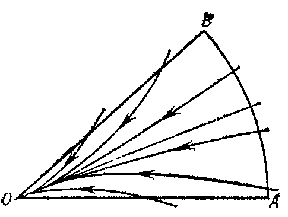
Figure: s083770d
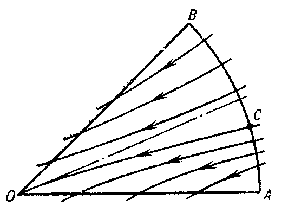
Figure: s083770e
Figure: s083770f
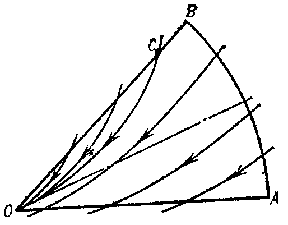
Figure: s083770g

Figure: s083770h
In a normal domain 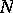 of any type the
of any type the 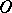 -curves tend to
-curves tend to 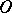 along the direction
along the direction 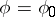 as
as 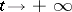 (or
(or 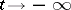 ), and with decreasing (increasing)
), and with decreasing (increasing) 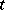 they leave the domain
they leave the domain 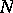 ; all other trajectories leave
; all other trajectories leave 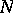 for both increasing and decreasing
for both increasing and decreasing 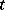 . The problems of distinguishing between the cases a) and b) for domains
. The problems of distinguishing between the cases a) and b) for domains 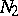 and
and 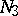 are called, respectively, the first and second distinction problems of Frommer.
are called, respectively, the first and second distinction problems of Frommer.
If a system
has at 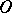 a finite number
a finite number 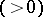 of exceptional directions, each of which can be included in a normal domain
of exceptional directions, each of which can be included in a normal domain 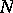 , and if for all domains
, and if for all domains 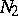 and
and 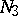 Frommer's distinction problems are solvable, then the topological structure of the arrangement of the trajectories of the system in a neighbourhood of
Frommer's distinction problems are solvable, then the topological structure of the arrangement of the trajectories of the system in a neighbourhood of 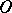 is completely explained, because the sectors with vertex
is completely explained, because the sectors with vertex 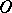 that are positioned between normal domains are, sufficiently close to
that are positioned between normal domains are, sufficiently close to  , entirely intersected by the trajectories of the system (as in Fig. h). Such a situation holds, for example, when
, entirely intersected by the trajectories of the system (as in Fig. h). Such a situation holds, for example, when
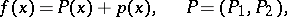 |
where 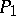 and
and 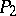 are forms of degree
are forms of degree 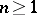 in the components
in the components 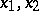 of the vector
of the vector  ,
,
 |
and when the following conditions are fulfilled: The form 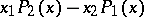 has real linear factors, the forms
has real linear factors, the forms 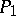 and
and 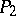 do not have common real linear factors, and
do not have common real linear factors, and  . Here situation a) holds in each of the domains
. Here situation a) holds in each of the domains  ,
, 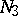 .
.
Analogues of Frommer normal domains have been introduced for systems of the form
of order 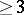 .
.
References
| [1] | M. Frommer, "Die Integralkurven einer gewöhnlichen Differentialgleichung erster Ordnung in der Umgebung rationaler Unbestimtheitsstellen" Math. Ann. , 99 (1928) pp. 222–272 |
| [2] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
| [3] | A.F. Andreev, "A uniqueness theorem for a normal region of Frommer's second type" Soviet Math. Dokl. , 3 : 1 (1962) pp. 132–135 Dokl. Akad. Nauk SSSR , 142 : 4 (1962) pp. 754–757 |
| [4] | A.F. Andreev, "Strengthening of the uniqueness theorem for an  -curve in -curve in 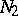 " Soviet Math. Dokl. , 3 : 5 (1962) pp. 1215–1216 Dokl. Akad. Nauk SSSR , 146 : 1 (1962) pp. 9–10 " Soviet Math. Dokl. , 3 : 5 (1962) pp. 1215–1216 Dokl. Akad. Nauk SSSR , 146 : 1 (1962) pp. 9–10 |
Sector in the theory of ordinary differential equations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sector_in_the_theory_of_ordinary_differential_equations&oldid=14776