Difference between revisions of "Sector in the theory of ordinary differential equations"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | s0837701.png | ||
| + | $#A+1 = 134 n = 2 | ||
| + | $#C+1 = 134 : ~/encyclopedia/old_files/data/S083/S.0803770 Sector in the theory of ordinary differential equations | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | An open curvilinear sector $ S $ | |
| + | with vertex at an isolated singular point $ O $ | ||
| + | of an [[Autonomous system|autonomous system]] of second-order ordinary differential equations | ||
| + | |||
| + | $$ \tag{* } | ||
| + | \dot{x} = f ( x),\ \ | ||
| + | x \in \mathbf R ^ {2} , | ||
| + | $$ | ||
| + | |||
| + | $ f \in C ( G) $, | ||
| + | where $ G $ | ||
| + | is the domain of uniqueness, that satisfies the following four conditions: 1) each lateral boundary of $ S $ | ||
| + | is a $ TO $- | ||
| + | curve of the system (*) (i.e. a semi-trajectory that approaches $ O $ | ||
| + | as $ | t | \rightarrow + \infty $, | ||
| + | and touches a certain direction at $ O $); | ||
| + | 2) the outer boundary of $ S $ | ||
| + | is a simple parametric arc (the homeomorphic image of a closed interval); 3) $ \overline{S}\; \setminus \{ 0 \} $ | ||
| + | does not contain singular points of (*). The fourth condition is one of the following three: 4a) all trajectories of the system (*) that start in $ S $ | ||
| + | leave this sector for both increasing and decreasing $ t $; | ||
| + | such a sector is called a hyperbolic sector, or a saddle sector (Fig. a); 4b) all trajectories of (*) that start in $ S $ | ||
| + | sufficiently near $ O $ | ||
| + | do not leave $ S $ | ||
| + | but approach $ O $ | ||
| + | as $ t $ | ||
| + | increases, and as $ t $ | ||
| + | decreases they leave $ S $( | ||
| + | or vice-versa); such a sector is called a parabolic sector or an open node sector (Fig. b); or 4c) all the trajectories of (*) that start in $ S $ | ||
| + | sufficiently near $ O $ | ||
| + | do not leave $ S $ | ||
| + | as $ t $ | ||
| + | increases or decreases but approach $ O $, | ||
| + | forming together with $ O $ | ||
| + | closed curves (loops), and for any two loops one encloses the other; such a sector is called an elliptic sector or a closed node sector (Fig. c). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s083770a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s083770a.gif" /> | ||
| Line 17: | Line 58: | ||
Figure: s083770c | Figure: s083770c | ||
| − | For any analytic system (*) with | + | For any analytic system (*) with $ TO $- |
| + | curves, a disc $ Q $ | ||
| + | of sufficiently small radius and centre at $ O $ | ||
| + | can always be divided into a finite number of sectors of a specific form: $ h $ | ||
| + | hyperbolic, $ p $ | ||
| + | parabolic and $ e $ | ||
| + | elliptic ones (see [[#References|[1]]] and [[#References|[2]]]). The [[Frommer method|Frommer method]] can be used to exhibit all these sectors, to determine the type of each, and to establish the rules of their succession in a circuit about $ O $ | ||
| + | along the boundary of $ Q $( | ||
| + | and thereby to show the topological structure of the arrangement of the trajectories of (*) in a neighbourhood of $ O $). | ||
| + | There are a priori estimates from above for $ h $, | ||
| + | $ p $ | ||
| + | and $ e $ | ||
| + | in terms of the order of smallness of the norm $ \| f ( x) \| $ | ||
| + | as $ x \rightarrow 0 $( | ||
| + | see [[#References|[1]]], [[#References|[4]]], [[#References|[5]]]). | ||
| − | Sometimes (see, for example, [[#References|[3]]]) the notion of a "sector" is defined more freely: In hyperbolic and parabolic sectors loops are allowed that cover a set without limit points on the rear boundary of a sector, and in elliptic sectors, loops that do not contain one another. Here the first sentence of the previous paragraph remains valid also for a system (*) of general form, and the Poincaré index | + | Sometimes (see, for example, [[#References|[3]]]) the notion of a "sector" is defined more freely: In hyperbolic and parabolic sectors loops are allowed that cover a set without limit points on the rear boundary of a sector, and in elliptic sectors, loops that do not contain one another. Here the first sentence of the previous paragraph remains valid also for a system (*) of general form, and the Poincaré index $ i $ |
| + | of the [[Singular point|singular point]] $ O $ | ||
| + | of (*) is expressed by Bendixson's formula | ||
| − | + | $$ | |
| + | i = 1 + | ||
| + | \frac{e - h }{2} | ||
| + | . | ||
| + | $$ | ||
====References==== | ====References==== | ||
| Line 31: | Line 92: | ||
A Frommer sector, or Frommer normal domain, is a circular sector | A Frommer sector, or Frommer normal domain, is a circular sector | ||
| − | + | $$ | |
| + | N = \ | ||
| + | \{ {( r, \phi ) } : {0 < r \leq \delta ,\ | ||
| + | | \phi - \phi _ {0} | \leq \epsilon } \} | ||
| + | $$ | ||
| − | with vertex at an isolated point | + | with vertex at an isolated point $ O $( |
| + | $ x = x _ {0} $) | ||
| + | of the system | ||
| − | (see 1)) with lateral boundary | + | (see 1)) with lateral boundary $ OA $ |
| + | and $ OB $, | ||
| + | $ \phi _ {A} = \phi _ {0} - \epsilon $, | ||
| + | $ \phi _ {B} = \phi _ {0} + \epsilon $, | ||
| + | and with the rear boundary $ AB $ | ||
| + | satisfying the following conditions (here $ r $ | ||
| + | and $ \phi $ | ||
| + | are polar coordinates in the $ x $- | ||
| + | plane with pole at $ O $, | ||
| + | and $ \delta , \epsilon , \phi _ {0} \in \mathbf R $): | ||
| − | A) | + | A) $ \phi = \phi _ {0} $ |
| + | is an exceptional direction of the system | ||
| − | at | + | at $ O $, |
| + | that is, there is a sequence $ x _ {k} = x _ {0} + ( r _ {k} \cos \phi _ {k} , r _ {k} \sin \phi _ {k} ) $, | ||
| + | $ k = 1 \dots $ | ||
| + | $ r _ {k} \rightarrow 0 $, | ||
| + | $ \phi _ {k} \rightarrow \phi _ {0} $ | ||
| + | as $ k \rightarrow + \infty $, | ||
| + | such that if $ \alpha ( x) $ | ||
| + | is the angle between the directions of the vectors $ f ( x) $ | ||
| + | and $ x - x _ {0} $, | ||
| + | then $ \mathop{\rm tan} \alpha ( x _ {k} ) \rightarrow 0 $ | ||
| + | as $ k \rightarrow + \infty $, | ||
| + | and this direction is unique in $ N $; | ||
| − | B) | + | B) $ \mathop{\rm tan} \alpha ( x) \neq 0 $ |
| + | for any $ x \in OA \cup OB $; | ||
| − | C) | + | C) $ \alpha ( x) \neq \pi /2 $ |
| + | for any $ x \in N $. | ||
| − | Suppose that the angle | + | Suppose that the angle $ \alpha ( x) $ |
| + | is measured from the vector $ x - x _ {0} $ | ||
| + | and has the sign of the reference direction. A sector $ N $ | ||
| + | is called a Frommer normal domain of the first type (notation: $ N _ {1} $) | ||
| + | if $ \mathop{\rm tan} \alpha ( x) < 0 $ | ||
| + | for $ x \in OA $ | ||
| + | and $ \mathop{\rm tan} \alpha ( x) > 0 $ | ||
| + | for $ x \in OB $; | ||
| + | a normal domain of the second type (notation: $ N _ {2} $) | ||
| + | if $ \mathop{\rm tan} \alpha ( x) > 0 $ | ||
| + | on $ OA $ | ||
| + | and $ \mathop{\rm tan} \alpha ( x) < 0 $ | ||
| + | on $ OB $; | ||
| + | and a normal domain of the third type $ ( N _ {3} ) $ | ||
| + | if $ \mathop{\rm tan} \alpha ( x) $ | ||
| + | has one and the same sign on $ OA $ | ||
| + | and on $ OB $. | ||
| + | These domains were introduced by M. Frommer [[#References|[1]]]. | ||
The trajectories of the system | The trajectories of the system | ||
| − | in Frommer normal domains behave as follows. The domain | + | in Frommer normal domains behave as follows. The domain $ N _ {1} $ |
| + | is covered by $ O $- | ||
| + | curves of the system (Fig. d). They form an open pencil (cf. [[Sheaf|Sheaf]] 2)), that is, a family of $ O $- | ||
| + | curves of the same type that depends continuously on a parameter which varies over an open interval. In the domain $ N _ {2} $ | ||
| + | there is either a) a unique $ O $- | ||
| + | curve (Fig. e), or b) infinitely many $ O $- | ||
| + | curves (a closed pencil; cf. Fig. f). In the domain $ N _ {3} $, | ||
| + | either a) there are infinitely many $ O $- | ||
| + | curves (a semi-open pencil; Fig. g) or b) there are no $ O $- | ||
| + | curves (Fig. h). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s083770d.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s083770d.gif" /> | ||
| Line 71: | Line 187: | ||
Figure: s083770h | Figure: s083770h | ||
| − | In a normal domain | + | In a normal domain $ N $ |
| + | of any type the $ O $- | ||
| + | curves tend to $ O $ | ||
| + | along the direction $ \phi = \phi _ {0} $ | ||
| + | as $ t \rightarrow + \infty $( | ||
| + | or $ t \rightarrow - \infty $), | ||
| + | and with decreasing (increasing) $ t $ | ||
| + | they leave the domain $ N $; | ||
| + | all other trajectories leave $ N $ | ||
| + | for both increasing and decreasing $ t $. | ||
| + | The problems of distinguishing between the cases a) and b) for domains $ N _ {2} $ | ||
| + | and $ N _ {3} $ | ||
| + | are called, respectively, the first and second distinction problems of Frommer. | ||
If a system | If a system | ||
| − | has at | + | has at $ O $ |
| + | a finite number $ (> 0) $ | ||
| + | of exceptional directions, each of which can be included in a normal domain $ N $, | ||
| + | and if for all domains $ N _ {2} $ | ||
| + | and $ N _ {3} $ | ||
| + | Frommer's distinction problems are solvable, then the topological structure of the arrangement of the trajectories of the system in a neighbourhood of $ O $ | ||
| + | is completely explained, because the sectors with vertex $ O $ | ||
| + | that are positioned between normal domains are, sufficiently close to $ O $, | ||
| + | entirely intersected by the trajectories of the system (as in Fig. h). Such a situation holds, for example, when | ||
| − | + | $$ | |
| + | f ( x) = P ( x) + p ( x),\ \ | ||
| + | P = ( P _ {1} , P _ {2} ), | ||
| + | $$ | ||
| − | where | + | where $ P _ {1} $ |
| + | and $ P _ {2} $ | ||
| + | are forms of degree $ n \geq 1 $ | ||
| + | in the components $ x _ {1} , x _ {2} $ | ||
| + | of the vector $ x $, | ||
| − | + | $$ | |
| + | p ( x) = o ( \| x \| ^ {n} ) \ \ | ||
| + | \textrm{ as } \| x \| \rightarrow 0, | ||
| + | $$ | ||
| − | and when the following conditions are fulfilled: The form | + | and when the following conditions are fulfilled: The form $ x _ {1} P _ {2} ( x) - x _ {2} P _ {1} ( x) $ |
| + | has real linear factors, the forms $ P _ {1} $ | ||
| + | and $ P _ {2} $ | ||
| + | do not have common real linear factors, and $ p \in C ^ {n + 1 } $. | ||
| + | Here situation a) holds in each of the domains $ N _ {2} $, | ||
| + | $ N _ {3} $. | ||
Analogues of Frommer normal domains have been introduced for systems of the form | Analogues of Frommer normal domains have been introduced for systems of the form | ||
| − | of order | + | of order $ \geq 3 $. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> M. Frommer, "Die Integralkurven einer gewöhnlichen Differentialgleichung erster Ordnung in der Umgebung rationaler Unbestimtheitsstellen" ''Math. Ann.'' , '''99''' (1928) pp. 222–272</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.F. Andreev, "A uniqueness theorem for a normal region of Frommer's second type" ''Soviet Math. Dokl.'' , '''3''' : 1 (1962) pp. 132–135 ''Dokl. Akad. Nauk SSSR'' , '''142''' : 4 (1962) pp. 754–757</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.F. Andreev, "Strengthening of the uniqueness theorem for an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083770/s083770136.png" />-curve in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083770/s083770137.png" />" ''Soviet Math. Dokl.'' , '''3''' : 5 (1962) pp. 1215–1216 ''Dokl. Akad. Nauk SSSR'' , '''146''' : 1 (1962) pp. 9–10</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M. Frommer, "Die Integralkurven einer gewöhnlichen Differentialgleichung erster Ordnung in der Umgebung rationaler Unbestimtheitsstellen" ''Math. Ann.'' , '''99''' (1928) pp. 222–272</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.F. Andreev, "A uniqueness theorem for a normal region of Frommer's second type" ''Soviet Math. Dokl.'' , '''3''' : 1 (1962) pp. 132–135 ''Dokl. Akad. Nauk SSSR'' , '''142''' : 4 (1962) pp. 754–757</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.F. Andreev, "Strengthening of the uniqueness theorem for an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083770/s083770136.png" />-curve in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083770/s083770137.png" />" ''Soviet Math. Dokl.'' , '''3''' : 5 (1962) pp. 1215–1216 ''Dokl. Akad. Nauk SSSR'' , '''146''' : 1 (1962) pp. 9–10</TD></TR></table> | ||
Latest revision as of 08:12, 6 June 2020
An open curvilinear sector $ S $
with vertex at an isolated singular point $ O $
of an autonomous system of second-order ordinary differential equations
$$ \tag{* } \dot{x} = f ( x),\ \ x \in \mathbf R ^ {2} , $$
$ f \in C ( G) $, where $ G $ is the domain of uniqueness, that satisfies the following four conditions: 1) each lateral boundary of $ S $ is a $ TO $- curve of the system (*) (i.e. a semi-trajectory that approaches $ O $ as $ | t | \rightarrow + \infty $, and touches a certain direction at $ O $); 2) the outer boundary of $ S $ is a simple parametric arc (the homeomorphic image of a closed interval); 3) $ \overline{S}\; \setminus \{ 0 \} $ does not contain singular points of (*). The fourth condition is one of the following three: 4a) all trajectories of the system (*) that start in $ S $ leave this sector for both increasing and decreasing $ t $; such a sector is called a hyperbolic sector, or a saddle sector (Fig. a); 4b) all trajectories of (*) that start in $ S $ sufficiently near $ O $ do not leave $ S $ but approach $ O $ as $ t $ increases, and as $ t $ decreases they leave $ S $( or vice-versa); such a sector is called a parabolic sector or an open node sector (Fig. b); or 4c) all the trajectories of (*) that start in $ S $ sufficiently near $ O $ do not leave $ S $ as $ t $ increases or decreases but approach $ O $, forming together with $ O $ closed curves (loops), and for any two loops one encloses the other; such a sector is called an elliptic sector or a closed node sector (Fig. c).

Figure: s083770a

Figure: s083770b

Figure: s083770c
For any analytic system (*) with $ TO $- curves, a disc $ Q $ of sufficiently small radius and centre at $ O $ can always be divided into a finite number of sectors of a specific form: $ h $ hyperbolic, $ p $ parabolic and $ e $ elliptic ones (see [1] and [2]). The Frommer method can be used to exhibit all these sectors, to determine the type of each, and to establish the rules of their succession in a circuit about $ O $ along the boundary of $ Q $( and thereby to show the topological structure of the arrangement of the trajectories of (*) in a neighbourhood of $ O $). There are a priori estimates from above for $ h $, $ p $ and $ e $ in terms of the order of smallness of the norm $ \| f ( x) \| $ as $ x \rightarrow 0 $( see [1], [4], [5]).
Sometimes (see, for example, [3]) the notion of a "sector" is defined more freely: In hyperbolic and parabolic sectors loops are allowed that cover a set without limit points on the rear boundary of a sector, and in elliptic sectors, loops that do not contain one another. Here the first sentence of the previous paragraph remains valid also for a system (*) of general form, and the Poincaré index $ i $ of the singular point $ O $ of (*) is expressed by Bendixson's formula
$$ i = 1 + \frac{e - h }{2} . $$
References
| [1] | I. Bendixson, "Sur des courbes définiés par des équations différentielles" Acta Math. , 24 (1901) pp. 1–88 |
| [2] | A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Qualitative theory of second-order dynamic systems" , Wiley (1973) (Translated from Russian) |
| [3] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
| [4] | A.N. Berlinskii, "On the structure of the neighborhood of a singular point of a two-dimensional autonomous system" Soviet Math. Dokl. , 10 : 4 (1969) pp. 882–885 Dokl. Akad. Nauk SSSR , 187 : 3 (1969) pp. 502–505 |
| [5] | M.E. Sagalovich, "Classes of local topological structures of an equilibrium state" Diff. Equations , 15 : 2 (1979) pp. 253–255 Differentsial'nye Urnveniya , 15 : 2 (1979) pp. 360–362 |
Comments
The lateral boundaries are sometimes called base solutions.
A Frommer sector, or Frommer normal domain, is a circular sector
$$ N = \ \{ {( r, \phi ) } : {0 < r \leq \delta ,\ | \phi - \phi _ {0} | \leq \epsilon } \} $$
with vertex at an isolated point $ O $( $ x = x _ {0} $) of the system
(see 1)) with lateral boundary $ OA $ and $ OB $, $ \phi _ {A} = \phi _ {0} - \epsilon $, $ \phi _ {B} = \phi _ {0} + \epsilon $, and with the rear boundary $ AB $ satisfying the following conditions (here $ r $ and $ \phi $ are polar coordinates in the $ x $- plane with pole at $ O $, and $ \delta , \epsilon , \phi _ {0} \in \mathbf R $):
A) $ \phi = \phi _ {0} $ is an exceptional direction of the system
at $ O $, that is, there is a sequence $ x _ {k} = x _ {0} + ( r _ {k} \cos \phi _ {k} , r _ {k} \sin \phi _ {k} ) $, $ k = 1 \dots $ $ r _ {k} \rightarrow 0 $, $ \phi _ {k} \rightarrow \phi _ {0} $ as $ k \rightarrow + \infty $, such that if $ \alpha ( x) $ is the angle between the directions of the vectors $ f ( x) $ and $ x - x _ {0} $, then $ \mathop{\rm tan} \alpha ( x _ {k} ) \rightarrow 0 $ as $ k \rightarrow + \infty $, and this direction is unique in $ N $;
B) $ \mathop{\rm tan} \alpha ( x) \neq 0 $ for any $ x \in OA \cup OB $;
C) $ \alpha ( x) \neq \pi /2 $ for any $ x \in N $.
Suppose that the angle $ \alpha ( x) $ is measured from the vector $ x - x _ {0} $ and has the sign of the reference direction. A sector $ N $ is called a Frommer normal domain of the first type (notation: $ N _ {1} $) if $ \mathop{\rm tan} \alpha ( x) < 0 $ for $ x \in OA $ and $ \mathop{\rm tan} \alpha ( x) > 0 $ for $ x \in OB $; a normal domain of the second type (notation: $ N _ {2} $) if $ \mathop{\rm tan} \alpha ( x) > 0 $ on $ OA $ and $ \mathop{\rm tan} \alpha ( x) < 0 $ on $ OB $; and a normal domain of the third type $ ( N _ {3} ) $ if $ \mathop{\rm tan} \alpha ( x) $ has one and the same sign on $ OA $ and on $ OB $. These domains were introduced by M. Frommer [1].
The trajectories of the system
in Frommer normal domains behave as follows. The domain $ N _ {1} $ is covered by $ O $- curves of the system (Fig. d). They form an open pencil (cf. Sheaf 2)), that is, a family of $ O $- curves of the same type that depends continuously on a parameter which varies over an open interval. In the domain $ N _ {2} $ there is either a) a unique $ O $- curve (Fig. e), or b) infinitely many $ O $- curves (a closed pencil; cf. Fig. f). In the domain $ N _ {3} $, either a) there are infinitely many $ O $- curves (a semi-open pencil; Fig. g) or b) there are no $ O $- curves (Fig. h).
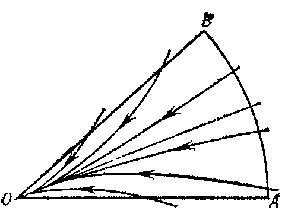
Figure: s083770d
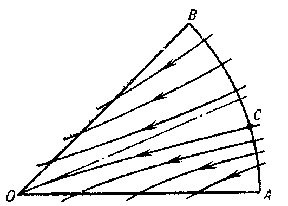
Figure: s083770e
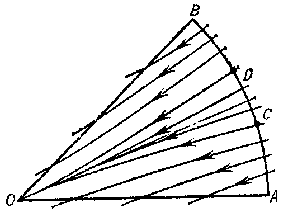
Figure: s083770f
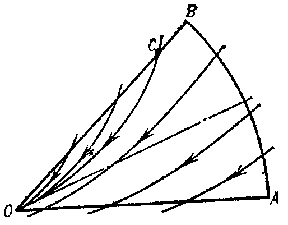
Figure: s083770g

Figure: s083770h
In a normal domain $ N $ of any type the $ O $- curves tend to $ O $ along the direction $ \phi = \phi _ {0} $ as $ t \rightarrow + \infty $( or $ t \rightarrow - \infty $), and with decreasing (increasing) $ t $ they leave the domain $ N $; all other trajectories leave $ N $ for both increasing and decreasing $ t $. The problems of distinguishing between the cases a) and b) for domains $ N _ {2} $ and $ N _ {3} $ are called, respectively, the first and second distinction problems of Frommer.
If a system
has at $ O $ a finite number $ (> 0) $ of exceptional directions, each of which can be included in a normal domain $ N $, and if for all domains $ N _ {2} $ and $ N _ {3} $ Frommer's distinction problems are solvable, then the topological structure of the arrangement of the trajectories of the system in a neighbourhood of $ O $ is completely explained, because the sectors with vertex $ O $ that are positioned between normal domains are, sufficiently close to $ O $, entirely intersected by the trajectories of the system (as in Fig. h). Such a situation holds, for example, when
$$ f ( x) = P ( x) + p ( x),\ \ P = ( P _ {1} , P _ {2} ), $$
where $ P _ {1} $ and $ P _ {2} $ are forms of degree $ n \geq 1 $ in the components $ x _ {1} , x _ {2} $ of the vector $ x $,
$$ p ( x) = o ( \| x \| ^ {n} ) \ \ \textrm{ as } \| x \| \rightarrow 0, $$
and when the following conditions are fulfilled: The form $ x _ {1} P _ {2} ( x) - x _ {2} P _ {1} ( x) $ has real linear factors, the forms $ P _ {1} $ and $ P _ {2} $ do not have common real linear factors, and $ p \in C ^ {n + 1 } $. Here situation a) holds in each of the domains $ N _ {2} $, $ N _ {3} $.
Analogues of Frommer normal domains have been introduced for systems of the form
of order $ \geq 3 $.
References
| [1] | M. Frommer, "Die Integralkurven einer gewöhnlichen Differentialgleichung erster Ordnung in der Umgebung rationaler Unbestimtheitsstellen" Math. Ann. , 99 (1928) pp. 222–272 |
| [2] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
| [3] | A.F. Andreev, "A uniqueness theorem for a normal region of Frommer's second type" Soviet Math. Dokl. , 3 : 1 (1962) pp. 132–135 Dokl. Akad. Nauk SSSR , 142 : 4 (1962) pp. 754–757 |
| [4] | A.F. Andreev, "Strengthening of the uniqueness theorem for an 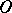 -curve in -curve in 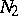 " Soviet Math. Dokl. , 3 : 5 (1962) pp. 1215–1216 Dokl. Akad. Nauk SSSR , 146 : 1 (1962) pp. 9–10 " Soviet Math. Dokl. , 3 : 5 (1962) pp. 1215–1216 Dokl. Akad. Nauk SSSR , 146 : 1 (1962) pp. 9–10 |
Sector in the theory of ordinary differential equations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sector_in_the_theory_of_ordinary_differential_equations&oldid=14776