Section of a mapping
From Encyclopedia of Mathematics

A mapping  for which
for which  . In a wider sense, a section of any morphism in an arbitrary category is a right-inverse morphism.
. In a wider sense, a section of any morphism in an arbitrary category is a right-inverse morphism.
Comments
If  is a subspace of
is a subspace of  , a section over
, a section over  of
of  is a mapping
is a mapping  such that
such that  for all
for all 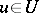 . For a vector bundle
. For a vector bundle 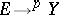 , where the mapping
, where the mapping 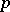 is part of the structure defined, one speaks of a section of the vector bundle
is part of the structure defined, one speaks of a section of the vector bundle 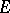 rather than of a section of
rather than of a section of 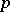 . This applies, e.g., also to sheaves and fibrations. A standard notation for the set of sections in such a case is
. This applies, e.g., also to sheaves and fibrations. A standard notation for the set of sections in such a case is 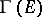 , or
, or 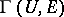 for the set of sections of
for the set of sections of 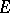 over
over 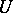 .
.
How to Cite This Entry:
Section of a mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Section_of_a_mapping&oldid=18495
Section of a mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Section_of_a_mapping&oldid=18495
This article was adapted from an original article by A.F. Kharshiladze (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article