Difference between revisions of "Second-order curve"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 74: | Line 74: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Aleksandrov, "Lectures on analytical geometry" , Moscow (1968) (In Russian) {{MR|0244836}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.V. Efimov, "A short course of analytical geometry" , Moscow (1967) (In Russian)</TD></TR></table> |
| Line 82: | Line 82: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Berger, "Geometry" , '''II''' , Springer (1987) {{MR|0903026}} {{MR|0895392}} {{MR|0882916}} {{MR|0882541}} {{ZBL|0619.53001}} {{ZBL|0606.51001}} {{ZBL|0606.00020}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H. Busemann, P.J. Kelly, "Projective geometry and projective metrics" , Acad. Press (1953) {{MR|0054980}} {{ZBL|0052.37305}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Coolidge, "A history of the conic sections and quadric surfaces" , Dover, reprint (1968) {{MR|0245397}} {{ZBL|0060.01006}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961) {{MR|1531486}} {{MR|0123930}} {{ZBL|0095.34502}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) {{MR|0046650}} {{ZBL|0047.38806}} </TD></TR></table> |
Latest revision as of 21:56, 30 March 2012
A plane curve whose rectangular Cartesian coordinates satisfy an algebraic equation of the second degree:
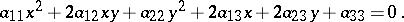 | (*) |
Equation (*) need not define a real geometrical form, but to preserve generality in such situations one says that it defines an imaginary second-order curve. Depending on the values of the coefficients of the equation (*) it can be transformed by parallel displacement and rotation of the coordinate system through some angle to one of the 9 canonical forms given below, to each of which there corresponds a definite class of curves. Namely,
non-degenerate curves:
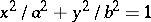 , ellipses (cf. Ellipse);
, ellipses (cf. Ellipse);
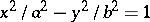 , hyperbolas (cf. Hyperbola);
, hyperbolas (cf. Hyperbola);
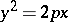 , parabolas (cf. Parabola);
, parabolas (cf. Parabola);
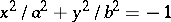 , imaginary ellipses;
, imaginary ellipses;
degenerate curves:
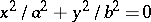 , pairs of imaginary intersecting lines;
, pairs of imaginary intersecting lines;
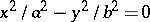 , pairs of real intersecting lines;
, pairs of real intersecting lines;
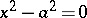 , pairs of real parallel lines;
, pairs of real parallel lines;
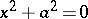 , pairs of imaginary parallel lines;
, pairs of imaginary parallel lines;
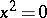 , a pair of coincident real lines.
, a pair of coincident real lines.
A second-order curve that has a unique centre of symmetry (the centre of the second-order curve) is called a central curve. The coordinates of the centre of a second-order curve are determined by the solution of the system
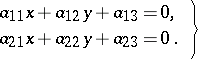 |
A second-order curve without a centre of symmetry or with an indefinite centre is called a non-central curve.
Investigations on the form of a second-order curve can be carried out without reducing the general equation to canonical form. This is done by considering the values of the so-called fundamental invariants of a second-order curve, that is, the following expressions in the coefficients of the equation (*), the values of which are not changed under a parallel displacement and a rotation of the coordinate system 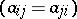 :
:
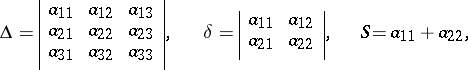 |
and the semi-invariant
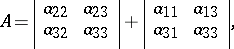 |
which is an invariant with respect to rotation of the coordinate system (see the Table below).
Many important properties of second-order curves can be studied by means of the characteristic quadratic form
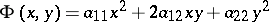 |
corresponding to equation (*). In particular, a non-degenerate second-order curve turns out to be an ellipse, an imaginary ellipse, a hyperbola, or a parabola, depending on whether 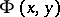 is a positive-definite, a negative-definite, an indefinite, or a semi-definite quadratic form. This can be established from the roots of its characteristic equation:
is a positive-definite, a negative-definite, an indefinite, or a semi-definite quadratic form. This can be established from the roots of its characteristic equation:
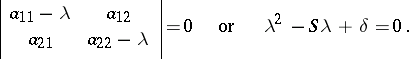 |
The three fundamental invariants 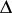 ,
, 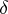 and
and 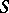 determine a second-order curve (excluding the case of parallel lines) up to a motion of the Euclidean plane: If the corresponding invariants
determine a second-order curve (excluding the case of parallel lines) up to a motion of the Euclidean plane: If the corresponding invariants 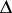 ,
, 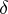 and
and 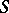 of two curves are equal, then these curves can be made to coincide by a motion. In other words, these curves are equivalent with respect to the group of motions of the plane (metrically equivalent).
of two curves are equal, then these curves can be made to coincide by a motion. In other words, these curves are equivalent with respect to the group of motions of the plane (metrically equivalent).
There is a classification of second-order curves from the point of view of other groups of transformations. Thus, with respect to the more general (than the group of motions) group of affine transformations any two curves defined by equations of the same canonical form are equivalent. For example, two similar second-order curves are regarded as equivalent. The connections between different affine classes of second-order curves make it possible to establish a classification from the point of view of projective geometry, in which elements at infinity do not play a special role. The real non-degenerate second-order curves, ellipses, hyperbolas, and parabolas, form one projective class — the class of real oval curves (ovals, cf. Oval). A real oval curve is an ellipse, hyperbola or parabola, depending on how it is situated with respect to the line at infinity; an ellipse intersects the line at infinity in two imaginary points, a hyperbola intersects it in two real points and a parabola touches it; there are projective transformations that take these curves into one another. There are 5 projective equivalence classes of second-order curves. Namely,
non-degenerate curves (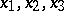 are the homogeneous coordinates):
are the homogeneous coordinates):
 , a real oval;
, a real oval;
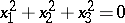 , an imaginary oval;
, an imaginary oval;
degenerate curves:
 , a pair of real lines;
, a pair of real lines;
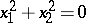 , a pair of imaginary lines;
, a pair of imaginary lines;
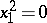 , a pair of coincident lines.
, a pair of coincident lines.
Apart from the analytic method of defining second-order curves (specifying the equation) there are other methods. For example, an ellipse, hyperbola and parabola can be obtained as a section of a conical surface by a plane (see Conic sections).'
<tbody> </tbody>
|
References
| [1] | P.S. Aleksandrov, "Lectures on analytical geometry" , Moscow (1968) (In Russian) MR0244836 |
| [2] | N.V. Efimov, "A short course of analytical geometry" , Moscow (1967) (In Russian) |
Comments
References
| [a1] | M. Berger, "Geometry" , II , Springer (1987) MR0903026 MR0895392 MR0882916 MR0882541 Zbl 0619.53001 Zbl 0606.51001 Zbl 0606.00020 |
| [a2] | H. Busemann, P.J. Kelly, "Projective geometry and projective metrics" , Acad. Press (1953) MR0054980 Zbl 0052.37305 |
| [a3] | J. Coolidge, "A history of the conic sections and quadric surfaces" , Dover, reprint (1968) MR0245397 Zbl 0060.01006 |
| [a4] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961) MR1531486 MR0123930 Zbl 0095.34502 |
| [a5] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
| [a6] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) MR0046650 Zbl 0047.38806 |
Second-order curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Second-order_curve&oldid=19170
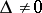
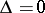
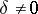 )
)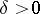
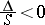 Real ellipses
Real ellipses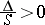 Imaginary ellipses
Imaginary ellipses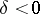
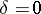 )
)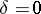
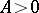 Pairs of imaginary parallel lines
Pairs of imaginary parallel lines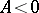 Pairs of real parallel lines
Pairs of real parallel lines Pairs of coincident parallel lines
Pairs of coincident parallel lines