Schwarz kernel

in the disc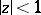

The function

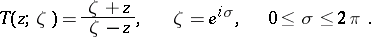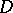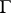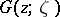Let be a finite simply-connected or multiply-connected domain with boundary , let be the Green function for the Laplace operator in 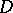, and let the real-valued function 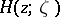be the conjugate to 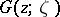. Then the function 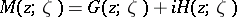is called the complex Green function of the domain 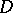. The function 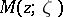is an analytic but multiple-valued (if 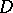is multiply connected) function of and a single-valued non-analytic function of 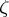. The function

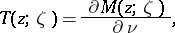where is the direction of the interior normal at 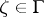, is called the Schwarz kernel of .

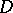Let 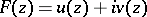be an analytic function without singular points in 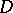, and let be single valued and continuous in 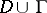. Then the following formula holds:

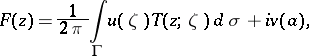where 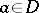is a fixed point and 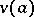is the value at of one of the branches of the function .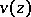

References

[1]	P.P. Zabreiko (ed.) A.I. Koshelev (ed.) M.A. Krasnoselskii (ed.) S.G. Mikhlin (ed.) L.S. Rakovshchik (ed.) V.Ya. Stet'senko (ed.) T.O. Shaposhnikova (ed.) R.S. Anderssen (ed.) , Integral equations - a reference text , Noordhoff (1975) (Translated from Russian)
[2]	S.G. Mikhlin, "Linear integral equations" , Hindushtan Publ. Comp. , Delhi (1960) (Translated from Russian)

Comments

Of course, some regularity conditions on 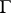have to be assumed, so that the normal derivative 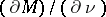is well defined. Note that the real part of 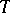is the Poisson kernel.

See also Schwarz integral.