Difference between revisions of "Schubert polynomials"
m (AUTOMATIC EDIT (latexlist): Replaced 50 formulas out of 58 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 58 formulas, 50 were replaced by TEX code.--> | Out of 58 formulas, 50 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
Polynomials introduced by A. Lascoux and M.-P. Schützenberger [[#References|[a18]]] as distinguished polynomial representatives of Schubert cycles (cf. also [[Schubert cycle|Schubert cycle]]) in the [[Cohomology ring|cohomology ring]] of the manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130110/s1301101.png"/> of complete flags in $\mathbf{C} ^ { n }$. This extended work by I.N. Bernshtein, I.M. Gel'fand and S.I. Gel'fand [[#References|[a1]]] and M. Demazure [[#References|[a8]]], who gave algorithms for computing representatives of Schubert cycles in the co-invariant algebra, which is isomorphic to the cohomology ring of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130110/s1301103.png"/> [[#References|[a6]]]: | Polynomials introduced by A. Lascoux and M.-P. Schützenberger [[#References|[a18]]] as distinguished polynomial representatives of Schubert cycles (cf. also [[Schubert cycle|Schubert cycle]]) in the [[Cohomology ring|cohomology ring]] of the manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130110/s1301101.png"/> of complete flags in $\mathbf{C} ^ { n }$. This extended work by I.N. Bernshtein, I.M. Gel'fand and S.I. Gel'fand [[#References|[a1]]] and M. Demazure [[#References|[a8]]], who gave algorithms for computing representatives of Schubert cycles in the co-invariant algebra, which is isomorphic to the cohomology ring of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130110/s1301103.png"/> [[#References|[a6]]]: | ||
Revision as of 17:44, 1 July 2020
Polynomials introduced by A. Lascoux and M.-P. Schützenberger [a18] as distinguished polynomial representatives of Schubert cycles (cf. also Schubert cycle) in the cohomology ring of the manifold  of complete flags in $\mathbf{C} ^ { n }$. This extended work by I.N. Bernshtein, I.M. Gel'fand and S.I. Gel'fand [a1] and M. Demazure [a8], who gave algorithms for computing representatives of Schubert cycles in the co-invariant algebra, which is isomorphic to the cohomology ring of
of complete flags in $\mathbf{C} ^ { n }$. This extended work by I.N. Bernshtein, I.M. Gel'fand and S.I. Gel'fand [a1] and M. Demazure [a8], who gave algorithms for computing representatives of Schubert cycles in the co-invariant algebra, which is isomorphic to the cohomology ring of  [a6]:
[a6]:
\begin{equation*} H ^ { * } ( F\operatorname{l} _ { n } , \mathbf{Z} ) \simeq \mathbf{Z} [ x _ { 1 } , \dots , x _ { n } ] / \mathbf{Z} ^ { + } [ x _ { 1 } , \dots , x _ { n } ] ^ { \mathcal{S} _ { n } }. \end{equation*}
Here, $\mathbf{Z} ^ { + } [ x _ { 1 } , \ldots , x _ { n } ] ^ { \mathcal{S} _ { n } }$ is the ideal generated by the non-constant polynomials that are symmetric in $x _ { 1 } , \ldots , x _ { n }$. See [a19] for an elegant algebraic treatment of Schubert polynomials, and [a13] and [a20] for a more geometric treatment.
For each $i = 1 , \dots , n - 1$, let $s_i$ be the transposition $( i , i + 1 )$ in the symmetric group $\mathcal{S} _ { n }$, which acts on $\mathbf{Z} [ x _ { 1 } , \ldots , x _ { n } ]$. The divided difference operator $\partial_{i}$ is defined by
\begin{equation*} \partial _ { i } f = \frac { f - s _ { i } f } { x _ { i } - x _ { i + 1} }. \end{equation*}
These satisfy
\begin{equation} \tag{a1} \left\{ \begin{array} { l } { \partial _ { i } ^ { 2 } = 0, } \\ { \partial _ { i } \partial _ { j } = \partial _ { j } \partial _ { i } \text { if } | i - j | > 1, } \\ { \partial _ { i } \partial _ { i + 1 } \partial _ { i } = \partial _ { i + 1 } \partial _ { i } \partial _ { i + 1 }. } \end{array} \right. \end{equation}
If $f _ { w } \in \mathbf{Z} [ x _ { 1 } , \dots , x _ { n } ]$ is a representative of the Schubert cycle 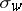 , then
, then
\begin{equation*} \partial _ { i }\, f _ { w } = \left\{ \begin{array} { l l } { 0 } & { \text{if} \ \text{l} ( s _ { i } w ) > \text{l} ( w ), } \\ { f _ { s _ { i } w } } & { \text{if} \ \text{l}( s _ { i } w ) < \text{l}( w ), } \end{array} \right. \end{equation*}
where $\mathbf{l} ( w )$ is the length of a permutation $w$ and $f _ { s _ { i } w }$ represents the Schubert cycle $\sigma _ { s _ { i } w} $. Given a fixed polynomial representative of the Schubert cycle 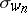 (the class of a point as $w _ { n } \in \mathcal{S}_n$ is the longest element), successive application of divided difference operators gives polynomial representatives of all Schubert cycles, which are independent of the choices involved, by (a1).
(the class of a point as $w _ { n } \in \mathcal{S}_n$ is the longest element), successive application of divided difference operators gives polynomial representatives of all Schubert cycles, which are independent of the choices involved, by (a1).
The choice of the representative 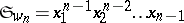 for
for 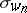 gives the Schubert polynomials. Since $\partial _ { n } \ldots \partial _ { 1 } \mathfrak { S } _ { w _ { n + 1 } } = \mathfrak { S } _ { w _ { n } }$, Schubert polynomials are independent of $n$ and give polynomials $\mathfrak { S } _ { w } \in \mathbf{Z} [ x _ { 1 } , x _ { 2 } , \ldots ]$ for $w \in \mathcal{S} _ { \infty } = \cup \mathcal{S} _ { n }$. These form a basis for this polynomial ring, and every Schur polynomial is also a Schubert polynomial.
gives the Schubert polynomials. Since $\partial _ { n } \ldots \partial _ { 1 } \mathfrak { S } _ { w _ { n + 1 } } = \mathfrak { S } _ { w _ { n } }$, Schubert polynomials are independent of $n$ and give polynomials $\mathfrak { S } _ { w } \in \mathbf{Z} [ x _ { 1 } , x _ { 2 } , \ldots ]$ for $w \in \mathcal{S} _ { \infty } = \cup \mathcal{S} _ { n }$. These form a basis for this polynomial ring, and every Schur polynomial is also a Schubert polynomial.
The transition formula gives another recursive construction of Schubert polynomials. For $w \in \mathcal{S} _ { \infty }$, let $r$ be the last descent of $w$ ($w ( r ) > w ( r + 1 ) < w ( r + 2 ) <\dots$) and define $s > r$ by $w ( s ) < w ( r ) < w ( s + 1 )$. Set $v = w ( r , s )$, where $( r , s )$ is the transposition. Then
\begin{equation*} \mathfrak { S } _ { w } = x _ { r } \mathfrak { S } _ { v } + \sum \mathfrak { S } _ { v ( q , r ) }, \end{equation*}
the sum over all $q < r$ with 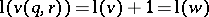 . This formula gives an algorithm to compute $\mathfrak { S } _ { w }$ as the permutations that appear on the right-hand side are either shorter than $w$ or precede it in reverse lexicographic order, and the minimal such permutation $u$ of length $m$ has $\mathfrak { S } _ { u } = x _ {1 } ^ {m }$.
. This formula gives an algorithm to compute $\mathfrak { S } _ { w }$ as the permutations that appear on the right-hand side are either shorter than $w$ or precede it in reverse lexicographic order, and the minimal such permutation $u$ of length $m$ has $\mathfrak { S } _ { u } = x _ {1 } ^ {m }$.
The transition formula shows that the Schubert polynomial $\mathfrak { S } _ { w }$ is a sum of monomials with non-negative integral coefficients. There are several explicit formulas for the coefficient of a monomial in a Schubert polynomial, either in terms of the weak order of the symmetric group [a3], [a5], [a12], an intersection number [a15] or the Bruhat order [a4]. An elegant conjectural formula of A. Kohnert [a16] remains unproven (as of 2000). The Schubert polynomial $\mathfrak { S } _ { w }$ for $w \in \mathcal{S} _ { n }$ is also the normal form reduction of any polynomial representative of the Schubert cycle 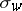 with respect to the degree-reverse lexicographic term order on $\mathbf{Z} [ x _ { 1 } , \ldots , x _ { n } ]$ with $x _ { 1 } < \ldots < x _ { n }$.
with respect to the degree-reverse lexicographic term order on $\mathbf{Z} [ x _ { 1 } , \ldots , x _ { n } ]$ with $x _ { 1 } < \ldots < x _ { n }$.
The above-mentioned results of [a6], [a1], [a8] are valid more generally for any flag manifold $G / B$ with $G$ a semi-simple reductive group and $B$ a Borel subgroup. When $G$ is an orthogonal or symplectic group, there are competing theories of Schubert polynomials [a2], [a10], [a17], each with own merits. There are also double Schubert polynomials suited for computations of degeneracy loci [a11], quantum Schubert polynomials [a9], [a7] and universal Schubert polynomials [a14].
References
| [a1] | I.N. Bernshtein, I.M. Gel'fand, S.I. Gel'fand, "Schubert cells and cohomology of the spaces $G / P$" Russian Math. Surveys , 28 : 3 (1973) pp. 1–26 |
| [a2] | S. Billey, M. Haiman, "Schubert polynomials for the classical groups" J. Amer. Math. Soc. , 8 : 2 (1995) pp. 443–482 |
| [a3] | S. Billey, W. Jockush, R. Stanley, "Some combinatorial properties of Schubert polynomials" J. Algebraic Combin. , 2 : 4 (1993) pp. 345–374 |
| [a4] | N. Bergeron, F. Sottile, "Skew Schubert functions and the Pieri formula for flag manifolds" Trans. Amer. Math. Soc. (to appear) |
| [a5] | N. Bergeron, "A combinatorial construction of the Schubert polynomials" J. Combin. Th. A , 60 (1992) pp. 168–182 |
| [a6] | A. Borel, "Sur la cohomologie des espaces fibrés principaux et des espaces homogènes des groupes de Lie compacts" Ann. Math. , 57 (1953) pp. 115–207 |
| [a7] | I. Ciocan–Fontanine, "On quantum cohomology rings of partial flag varieties" Duke Math. J. , 98 : 3 (1999) pp. 485–524 |
| [a8] | M. Demazure, "Désingularization des variétés de Schubert généralisées" Ann. Sci. École Norm. Sup. (4) , 7 (1974) pp. 53–88 |
| [a9] | S. Fomin, S. Gelfand, A. Postnikov, "Quantum Schubert polynomials" J. Amer. Math. Soc. , 10 (1997) pp. 565–596 |
| [a10] | S. Fomin, A.N. Kirillov, "Combinatorial $B _ { n }$-analogs of Schubert polynomials" Trans. Amer. Math. Soc. , 348 (1996) pp. 3591–3620 |
| [a11] | W. Fulton, P. Pragacz, "Schubert varieties and degeneracy loci" , Lecture Notes in Mathematics , 1689 , Springer (1998) |
| [a12] | S. Fomin, R. Stanley, "Schubert polynomials and the nilCoxeter algebra" Adv. Math. , 103 (1994) pp. 196–207 |
| [a13] | W. Fulton, "Young tableaux" , Cambridge Univ. Press (1997) |
| [a14] | W. Fulton, "Universal Schubert polynomials" Duke Math. J. , 96 : 3 (1999) pp. 575–594 |
| [a15] | A. Kirillov, T. Maeno, "Quantum double Schubert polynomials, quantum Schubert polynomials, and the Vafa–Intriligator formula" Discr. Math. , 217 : 1–3 (2000) pp. 191–223 (Formal Power Series and Algebraic Combinatorics (Vienna, 1997)) |
| [a16] | A. Kohnert, "Weintrauben, polynome, tableaux" Bayreuth Math. Schrift. , 38 (1990) pp. 1–97 |
| [a17] | A. Lascoux, P. Pragacz, J. Ratajski, "Symplectic Schubert polynomials à la polonaise, appendix to operator calculus for $\widetilde{Q}$-polynomials and Schubert polynomials" Adv. Math. , 140 (1998) pp. 1–43 |
| [a18] | A. Lascoux, M.-P. Schützenberger, "Polynômes de Schubert" C.R. Acad. Sci. Paris , 294 (1982) pp. 447–450 |
| [a19] | I.G. Macdonald, "Notes on Schubert polynomials" Lab. Combin. et d'Inform. Math. (LACIM) Univ. Québec (1991) |
| [a20] | L. Manivel, "Fonctions symétriques, polynômes de Schubert et lieux de dégénérescence" Cours Spécialisés Soc. Math. France , 3 (1998) |
Schubert polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schubert_polynomials&oldid=50707