Schrödinger representation
One of the basic possible (together with the Heisenberg representation and the interaction representation (cf. Interaction, representation of)) equivalent representations of the dependence on time  of operators
of operators  and wave functions
and wave functions  in quantum mechanics and quantum field theory. In the Schrödinger representation the operators
in quantum mechanics and quantum field theory. In the Schrödinger representation the operators  corresponding to physical dynamical quantities do not depend on
corresponding to physical dynamical quantities do not depend on  ; thus, the solution of the Schrödinger equation
; thus, the solution of the Schrödinger equation
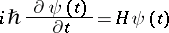 | (1) |
can be formally expressed by the Hamilton operator  , which is independent of
, which is independent of  , in the form
, in the form
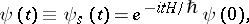 | (2) |
where  , being the initial value, does not depend on time, and the wave function in the Schrödinger representation depends on
, being the initial value, does not depend on time, and the wave function in the Schrödinger representation depends on 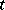 and contains all information with respect to changes in the state of the system when
and contains all information with respect to changes in the state of the system when  changes. The mean value of the operator
changes. The mean value of the operator  in the Schrödinger representation
in the Schrödinger representation
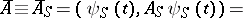 | (3) |
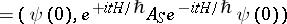 |
depends on  as a result of the dependence on
as a result of the dependence on 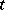 of the wave functions
of the wave functions 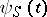 .
.  can be also considered as the mean value of the time-dependent operator
can be also considered as the mean value of the time-dependent operator 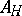 over the wave functions
over the wave functions 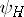 , which do not depend on
, which do not depend on 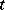 :
:
 | (4) |
i.e. as the mean value of an operator in the Heisenberg representation. The invariance property of the mean value (which should be observable and have physical meaning) under unitary transformations of type (4) means that the Schrödinger representation, the Heisenberg representation and the interaction representation are equivalent.
The Schrödinger representation was called after E. Schrödinger, who introduced it in 1926 when formulating an equation in quantum mechanics that was later called the Schrödinger equation.
Comments
Instead of Schrödinger representation one uses sometimes Schrödinger picture.
Equation (2) is correct for time-independent Hamiltonian operators only (cf. Schrödinger equation).
Schrödinger representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schr%C3%B6dinger_representation&oldid=17978