Schröder functional equation
From Encyclopedia of Mathematics
The equation
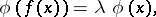 | (a1) |
where 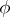 is the unknown function and
is the unknown function and 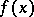 is a known real-valued function of a real variable
is a known real-valued function of a real variable  . I.e. one asks for the eigenvalues and eigenfunctions of the composition operator (substitution operator)
. I.e. one asks for the eigenvalues and eigenfunctions of the composition operator (substitution operator) 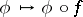 . Sometimes
. Sometimes 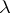 is allowed to be a function itself.
is allowed to be a function itself.
One also considers the non-autonomous Schröder functional equation
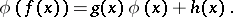 |
The Schröder and Abel functional equations (see also Functional equation) have much to do with the translation functional equation
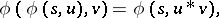 |
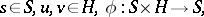 |
where 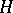 is a semi-group, which asks for something like a right action of
is a semi-group, which asks for something like a right action of 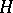 on
on  , [a1], [a4].
, [a1], [a4].
The equation was formulated by E. Schröder, [a5], and there is an extensive body of literature.
References
| [a1] | J. Aczél, "A short course on functional equations" , Reidel (1987) |
| [a2] | M. Kuczma, "On the Schröder operator" , PWN (1963) |
| [a3] | M. Kuczma, "Functional equations in a single variable" , PWN (1968) |
| [a4] | G. Targonski, "Topics in iteration theory" , Vandenhoeck and Ruprecht (1981) pp. 82ff. |
| [a5] | E. Schröder, "Uber iterierte Funktionen III" Math. Ann. , 3 (1970) pp. 296–322 |
| [a6] | J. Walorski, "Convex solutions of the Schröder equation in Banach spaces" Proc. Amer. Math. Soc. , 125 (1997) pp. 153–158 |
How to Cite This Entry:
Schröder functional equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schr%C3%B6der_functional_equation&oldid=15050
Schröder functional equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schr%C3%B6der_functional_equation&oldid=15050
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article